Monográfico
Evaluación de un juego serio que contribuye a fortalecer el razonamiento lógico-matemático en estudiantes de nivel medio superior
Assessment of a serious game that may contribute to improving logical-mathematical reasoning in high school students
Evaluación de un juego serio que contribuye a fortalecer el razonamiento lógico-matemático en estudiantes de nivel medio superior
RIED. Revista Iberoamericana de Educación a Distancia, vol. 24, núm. 1, 2021
Asociación Iberoamericana de Educación Superior a Distancia
Recepción: 06 Mayo 2020
Aprobación: 31 Julio 2020
Cómo referenciar este artículo: López Sánchez, A., y González Lara, A. (2021). Evaluación de un juego serio que contribuye a fortalecer el razonamiento lógico-matemático en estudiantes de nivel medio
superior. RIED. Revista Iberoamericana de Educación a
Distancia, 24(1)), pp. 221-243. doi: http://dx.doi.org/10.5944/ried.24.1.27450
Resumen: Actualmente, contar con habilidades para resolver problemas usando el razonamiento lógico-matemático es muy importante para el desarrollo de la ciencia y la tecnología. De acuerdo con los resultados de pruebas como el Programa para la Evaluación Internacional de Alumnos (PISA) y Plan Nacional para la Evaluación de los Aprendizajes (PLANEA), en México los estudiantes se encuentran en un dominio insuficiente en este razonamiento debido a que conocen los conceptos, pero no saben cómo aplicarlos. Para contribuir a resolver este problema, en esta investigación se presenta la evaluación de un juego serio (el cual contiene problemas de opción múltiple) para fortalecer el razonamiento lógico-matemático con la implementación de un sistema basado en lógica difusa. Para lograr lo anterior se diseñaron dos exámenes similares en cuanto complejidad y el tiempo máximo de respuesta. Posteriormente se aplicó la primera prueba y después se les proporcionó a 33 estudiantes de nivel medio superior el juego, los cuales lo utilizaron durante dos semanas y finalmente se aplicó la segunda prueba. Se analizaron los resultados de las pruebas con base en el tiempo invertido y los niveles alcanzados durante el uso del juego, se encontró que la mayoría de los estudiantes pueden hacer procedimientos lineales, pero se les dificulta hacer múltiples procedimientos, también se identificó que los estudiantes que utilizaron el juego o avanzaron de nivel mejoraron a diferencia de los que no lo hicieron.
Palabras clave: aprendizaje, tecnología de la información, inteligencia artificial.
Abstract: Nowadays, having skills to solve problems using logical-mathematical reasoning is very important for the development of science and technology. According to the results of tests like the Program for International Student Assessment (PISA) and the National Plan for Learning Assessment (PLANEA), students in Mexico have a poor command in this type of reasoning, since they know the concepts but they do not know how to apply them. To help in solving this problem, this research presents the assessment of a serious game (which contains multiple-choice problems) to strengthen the logical-mathematical reasoning with the implementation of a system based on fuzzy logic. To achieve the above, two exams which were similar in ability level and time limit were designed and maximum time to answer. Afterward, the first test was applied and then the 33 high-school students were provided with the game, which they used for two weeks and finally the second test was applied. The results from the tests were analyzed based on the duration and the levels reached during the use of the game, it was discovered that most of the students can do linear procedures, but they find it difficult to do multiple procedures. Also, it was identified that those students that used the game or moved to the next level improved their performance, unlike those who did not use it.
Keywords: learning, information technology, artificial intelligence.
Actualmente, contar con habilidades matemáticas es muy importante, debido a que los estudiantes pueden interpretar textos, realizar cálculos, operaciones e incluso análisis de situaciones, logrando así resolver problemas ya sean cotidianos o de una carrera profesional con ayuda de conocimientos previos (Soto, 2018).
El pensamiento es una actividad mental que requiere esfuerzo y es impulsado cuando el individuo se encuentra en una situación que requiere una planeación para alcanzar una meta, por lo que se desarrolla en los adolescentes y adultos, facilitando la resolución de problemas matemáticos, aunque este pensamiento es necesario, también se afirma que no es suficiente debido a que existe un gran número de personas que no han logrado mejorar esa habilidad conocida como razonamiento lógico matemático, ya que solo saben resolver operaciones básicas sin saber cómo, cuándo y en qué casos aplicarlas (Quintero, Suárez, García y Vanegas, 2012; Larrazolo, Backhoff y Tirado, 2013).
Se puede decir que el razonamiento lógico-matemático es la capacidad para resolver problemas así como realizar deducciones con el propósito de establecer soluciones con argumentos válidos, por lo que cuando las personas tienen un buen razonamiento pueden emplear fórmulas, experimentar y resolver problemas en su vida cotidiana (Rodríguez, Mendivil, Arámburo y Valenzuela, 2017).
En 2018, México participó (en unión con 78 países) en el Programa para la Evaluación Internacional de Alumnos (PISA), con la participación de 600,000 estudiantes representando alrededor de 32 millones de jóvenes de 15 años de las diferentes instituciones del mundo, en esta evaluación, una de las áreas incluidas es el uso y la interpretación de matemáticas en distintas situaciones, incluyendo el razonamiento y aplicación de conocimiento; México fue posicionado en lugar 55, con un promedio de 409 puntos en el área de matemáticas, lo cual lo coloca debajo del promedio establecido por la Organización para la Cooperación y el Desarrollo Económico (OCDE) de 489 puntos, lo que significa que solamente uno de cada 100 estudiantes mexicanos obtiene un rendimiento de nivel superior (OECD, 2018).
No solamente se han realizado pruebas de manera internacional, en 2017 participaron 117,700 estudiantes de 2,319 escuelas en la evaluación del Plan Nacional para la Evaluación de los Aprendizajes (PLANEA) desarrollado por el Instituto Nacional para la Evaluación de la Educación (INEE), en esta evaluación, el área de matemáticas se encuentra conformada por 52 reactivos de sentido numérico y pensamiento algebraico, 51 de cambios y relaciones, 13 de forma, espacio y medida, así como también 32 de manejo de la información; los resultados que se obtuvieron indican que seis de cada diez alumnos se encuentran en el nivel I (66%), dos de cada diez en el nivel II (23%), ocho de cada 100 (8%) en el nivel III y casi tres de cada 100 (2.5%) en el último nivel, lo anterior representa que el 66% de los estudiantes evaluados tiene dificultades para realizar operaciones con fracciones y/o variables (INEE, 2019a).
El Instituto Nacional para la Evaluación de la Educación (INEE) establece que el 59% de los estudiantes de sexto de primaria, el 64.5% de los alumnos de tercero de secundaria y el 66.2% de los estudiantes que terminan la educación media superior se encuentran en un dominio insuficiente en el área de matemáticas, el reporte indica que los estudiantes de educación media superior tienen dificultades para realizar operaciones con fracciones, que combinen incógnitas y/o variables ( INEE, 2019b ).
Para solucionar este problema Bragdon y Fellows (2003) proponen ejercicios mentales con el propósito de desafiar las destrezas en la vida real como el razonamiento lógico-deductivo, la manipulación de símbolos y las reglas de cálculo matemático, con apoyo de libros, herramientas informáticas o incluso juegos serios (Michael y Chen, 2006; Alvarez y Djaouti, 2011) por lo que muchos de los estudiantes cursan tutorías con el objetivo de resolver problemas relacionados con la dificultad de aprendizaje o incluso habilidades de estudio (García, Cuevas, Vales y Cruz, 2012) ya sea de manera física o a través de plataformas virtuales como Moodle (Moodle, 2020), Structuralia (Structuralia, 2020) y evolCampus (EvolMind, 2020).
Sin embargo, aunque los estudiantes conozcan las operaciones y los conceptos no saben cómo utilizarlos debido a que en la mayoría de las aplicaciones los usuarios responden a una serie de preguntas con ayuda de libros o internet.
El objetivo de la investigación que se presenta en este trabajo es evaluar un juego serio cuyo propósito consiste en fortalecer el razonamiento lógico matemático, implementando un sistema basado en lógica difusa, con los siguientes objetivos específicos:
- Diseñar dos evaluaciones con los mismos niveles de dificultad, pero con distintos problemas.
- Aplicar las dos evaluaciones, una antes y la otra después de utilizar el juego serio.
- Comparar los resultados de las dos evaluaciones con base en el tiempo y los aciertos obtenidos para cada examen.
Como se mencionó anteriormente, en este artículo no solamente se diseñarán y aplicarán dos evaluaciones (una antes y la otra después de usar el juego serio), sino que también se analizarán los resultados y el tiempo en que tardaron en contestar las evaluaciones con respecto al tiempo invertido en utilizar el juego serio, los subtemas terminados completando los tres niveles, así como también cuantos subtemas se avanzaron por lo menos al siguiente nivel (nivel 2), para posteriormente determinar si los estudiantes mejoraron o no al usar el juego.
La motivación de este artículo es demostrar que un juego serio con implementación de un sistema basado en lógica difusa ayuda a fortalecer el razonamiento lógico matemático, por lo que para esta investigación se utilizaran estudiantes de nivel medio superior.
LIMITACIONES
Esta investigación se realizó con un tamaño de muestra inicial, obteniendo resultados preliminares, sin embargo, se busca ampliar el tamaño de muestra por parte de los estudiantes de nivel medio superior.
TRABAJOS RELACIONADOS
Se han utilizado juegos serios para el aprendizaje de las matemáticas como MathFraction, el cual consiste en enseñar fracciones a niños de primaria, enfocado al contexto regional del lugar (Ibarra, Soto, Ataucusi y Ataucusi, 2016), NNG (Number Navigation Game), en donde su objetivo consiste en fortalecer la solución de problemas aritméticos en estudiantes de cuarto, quinto y sexto año de primaria ( Brezovszky et al., 2019) o MathBharata, el cual está dirigido a niños con discapacidad intelectual y se compone de cinco preguntas por competencia con dos minutos para contestar cada uno de los problemas, compuestos principalmente por números en lugar de oraciones (Mangowal, Yuhana, Yuniarno y Purnomo, 2017).
No solo se utilizan los juegos serios para el desarrollo de aplicaciones con un propósito serio, sino que también existen aplicaciones usando inteligencia artificial (IA), como el Multiagents Intelligent Tutoring Systems el cual consiste en problemas de programación lineal (Soares, Gonçalves, Monteiro, Machado y Jusan, 2016).
RAZONAMIENTO LÓGICO-MATEMÁTICO
Gardner y Hatch (1989) definen la inteligencia lógica matemática como la capacidad de resolver problemas, comprender patrones y manejar cadenas de razonamiento. El Consejo Nacional de Profesores de Matemáticas (NCTM, National Council of Teachers of Mathematics) de Estados Unidos, define que el razonamiento lógico matemático requiere de habilidades para construir conjeturas, desarrollar y evaluar argumentos, así como también de seleccionar y utilizar diferentes tipos de representación matemática (Kramarski y Mevarech, 2003).
Se puede decir que el razonamiento lógico matemático es la capacidad de comprender datos usando proposiciones y funciones para la categorización, distribución y deducción de pruebas de hipótesis empleando una serie de pasos (Armstrong, 2006; Lithner, 2000):
- Paso 1: Se cumple una situación problemática.
- Paso 2: Se define una estrategia para resolver el problema.
- Paso 3: Se implementa la estrategia (en caso de no resolver regresar al anterior).
- Paso 4: Se obtiene un resultado.
El razonamiento matemático es la disciplina que subyace de las matemáticas, la ciencia y la tecnología, se emplea para hacer deducciones a partir de hipótesis con base en reglas, leyes y principios morales, por lo que se utiliza en la ingeniería inversa, programación, en tecnologías de la información, entre otras profesiones relacionadas con la ingeniería (Johnson, Khemlani y Goodwin, 2015; Holvikivi, 2007).
EL APRENDIZAJE
El proceso de enseñanza-aprendizaje ha cambiado a lo largo del tiempo, por lo que se emplean distintas maneras de adquirir el conocimiento con el propósito de que las personas puedan acceder, codificar, recuperar y usar la información en distintas situaciones (Hurtado, García, Rivera y Forgiony, 2018).
Con el propósito de comparar el nivel de aprendizaje logrado con el material proporcionado se realizan evaluaciones, se puede decir que una evaluación es una actividad orientada a determinar el mérito o valor, en otras palabras, consiste en comparar los datos obtenidos de algo a través de un proceso sistemático, formulando un juicio de valor sobre el resultado final y es utilizado en múltiples objetos (profesores, alumnos, productos, entre otros) (Fernández, 2014). Existen diferentes instrumentos para el proceso de evaluación del aprendizaje, los cuales se pueden apreciar a continuación (Santibáñez, 2016):
-
Pruebas orales: Es la forma más antigua de evaluación y consiste en dar respuestas de manera oral a preguntas de una o más personas que aplican el examen, permitiendo el desarrollo de habilidades de comunicación con respuestas más auténticas (
Huxham, Campbell y Westwood, 2010).
- Estructuración autónoma: consiste en realizar una exposición oral sobre algún tópico con base en la secuencia, extensión y profundidad que el estudiante determine.
- Estructuración cerrada: consiste en realizar una serie de preguntas (entre dos a cinco preguntas por alumno) a un grupo de estudiantes de manera alterna o sucesivamente en un rango de tiempo establecido.
-
Pruebas escritas: estas pruebas son las más utilizadas por los maestros, en donde usualmente evalúan y califican el aprendizaje alcanzado por parte de los estudiantes (Jarero,
Aparicio y Sosa, 2013).
- Ítems de respuesta libre: otorgan libertad para expresar la respuesta.
- Ítems de respuesta breve: se presentan por preguntas realizadas en forma directa, considerando una respuesta breve.
- Ítems de opción simple: el alumno decide entre dos opciones como verdadero-falso, si-no, entre otros.
- Ítems de opción triple: son similares a los ítems de opción simple, pero con la opción de interponer otro termino.
- Ítems de opción múltiple: su estructura consiste principalmente de un enunciado seguido por cuatro o cinco posibles elecciones de respuesta.
Con base en las evaluaciones mencionadas anteriormente, se determinó realizar exámenes escritos de opción múltiple, por ser más eficaces para medir y evaluar el aprendizaje debido a que se pueden realizar procedimientos (por lo que destacan en áreas como ciencias) a los problemas establecidos, así como también generan menos nervios, ansiedad y más tiempo para elaborar su respuesta ( Lasso y Córdoba, 2015; Santibáñez, 2016).
Pruebas - Test para las muestras de datos
Se utilizan pruebas Welch con el propósito de conocer si en dos poblaciones existe una diferencia significativa entre las medias poblacionales con varianzas y tamaños diferentes, donde x1 y x2 son las medias de las muestras, sx1 y sx2 son las varianzas estimadas, así como también n1 y n2 son los tamaños para cada grupo de manera independiente (Aishah y Syed, 2014; Delacre, Lakens y Leys, 2017):
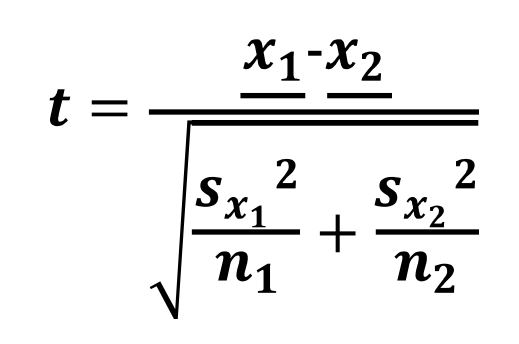
Para calcular los grados de libertad se utiliza lo siguiente:
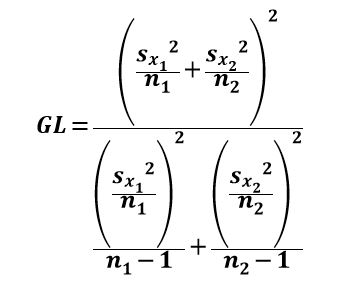
En algunas ocasiones el resultado obtenido para determinar los grados de libertad no necesariamente es un entero, por lo que se considera el valor entero más cercano.
ESTRUCTURA DEL JUEGO SERIO
El juego serio a evaluar tiene como nombre “MathLogic - La Leyenda de YuZhen” como se muestra en la figura 1 la estructura del juego, el cual está conformado con un estilo caricaturesco y definido en un mundo encantado con ayuda de cuatro personajes (uno al inicio del juego y otro para cada tema del juego), en donde solicitan la ayuda del jugador a través de diálogos de texto informando la situación en la que se encuentran y la manera de cómo ayudarlos (pasando todas las misiones del tema de cada personaje).
La estructura del juego se encuentra definida con base en el Examen Nacional de Ingreso a la Educación Superior (EXANI-II) por el Centro Nacional de Evaluación para la Educación Superior (Ceneval) en México, donde se estructura se puede observar en la figura 2 (López, 2017).
Se recopilaron a través de distintas fuentes de información como libros, guías de ingreso a las distintas escuelas e incluso en internet, los problemas de matemáticas que conforman el juego serio, los cuales posteriormente fueron analizados, rechazados o aceptados y clasificados en cada uno de los subtemas por un grupo de expertos en el área, todos ellos son licenciados en matemáticas por la Facultad de Ciencias Físico Matemáticas de la Universidad Autónoma de Nuevo León en México, como se muestra en la tabla 1.
| Experto | Experiencia |
| Experto 1 | Tres años trabajando en la Dirección de Evaluación Institucional del TecMilenio, como especialista en evaluación y revisión de exámenes online de matemáticas, tres años en la evaluación de maestros para la elaboración de reactivos de la misma área y tres años impartiendo asesorías en la FCFM a nivel licenciatura. |
| Experto 2 | Dos años como evaluador en actividades en el desarrollo de creatividad y capacidad para resolución de problemas de nivel medio superior (CBTas), tres años y medio impartiendo asesorías para nivel superior en la FCFM, siete años en el desarrollo de soluciones basadas en modelos matemáticos. |
| Experto 3 | Veinte años impartiendo clases para la FCFM en el área de matemáticas, con un doctorado en Ciencias con Orientación en Matemáticas y una línea de desarrollo de álgebras y las ecuaciones diferenciales, así como también integrante del Cuerpo Académico de Sistemas Complejos. |
Asimismo, se establecieron tres niveles de dificultad, definidos en la tabla 2, los cuales se establecieron con apoyo del mismo grupo de expertos y una guía titulada “Niveles de dominio en Habilidad matemática” (Reyes, Castillo, Zúñiga y Llarena, 2012).
| Nivel | Características |
| 1 (Bajo) | Su nivel de razonamiento se caracteriza por lograr resolver problemas utilizando una aplicación de conocimientos y procedimientos lineales. |
| 2 (Intermedio) | Se caracteriza por tener un nivel de razonamiento en el cual se logran ejecutar múltiples procedimientos, incluyendo decisiones secuenciales. |
| 3 (Alto) | Consiste en poseer un nivel de razonamiento, logrando proponer y evaluar soluciones justificando su utilización y entender el lenguaje simbólico, logrando formar modelos y estrategias con base en observación y análisis. |
Todos los problemas reestructurados se almacenaron en una base de datos (BD) sin perder la lógica del problema con base en diferentes libros o páginas de internet recopilados, validados y clasificados por el grupo de expertos, como se muestra en la figura 3, un problema del subtema de Jerarquía de operaciones.
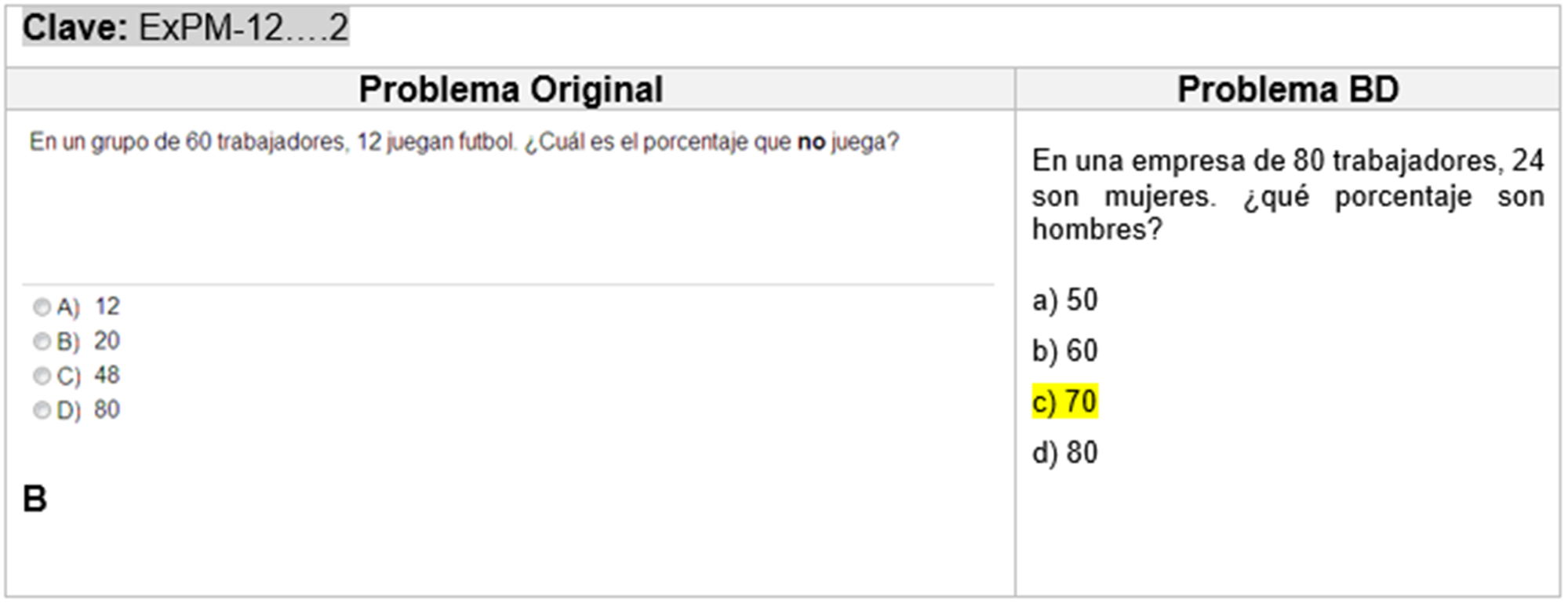
En total se reestructuraron 231 problemas para los diferentes temas, subtemas y niveles como se muestra en la tabla 3.
| Tema | Subtema | Nivel 1 | Nivel 2 | Nivel 3 | Total |
| Razonamiento aritmético | Jerarquía de operaciones básicas | 9 | 12 | 8 | 29 |
| Relaciones de proporcionalidad | 7 | 8 | 7 | 22 | |
| Razonamiento algebraico | Expresiones algebraicas | 11 | 8 | 8 | 27 |
| Productos notables | 6 | 6 | 6 | 18 | |
| Ecuaciones | 10 | 8 | 7 | 25 | |
| Sistemas de ecuaciones | 6 | 10 | 7 | 23 | |
| Representaciones gráficas | 7 | 8 | 9 | 24 | |
| Razonamiento estadístico y probabilístico | Frecuencias e información grafica | 6 | 7 | 7 | 20 |
| Medidas descriptivas | 7 | 8 | 6 | 21 | |
| Nociones de probabilidad | 9 | 7 | 6 | 22 |
Para el proceso de evaluación del juego serio se desarrolló e implementó un Sistema de Inferencia Difuso (FIS, Fuzzy Inference System) compuesto de tres variables y para cada variable tres etiquetas lingüísticas, en donde el usuario contesta una misión compuesta de cinco problemas de opción múltiple de orden aleatorio (tanto los problemas como sus soluciones) obteniendo un resultado (variable de salida) de si se regresa, avanza o se queda en el mismo nivel de complejidad con base en el tiempo que tardó en contestar y su respuesta (variables de entrada).
1. Variables de entrada
-
Tiempo: duración estimada para responder cada problema con un tiempo mínimo y máximo de respuesta almacenado en la BD, es decir cada problema tiene un tiempo estimado de respuesta dependiendo de la complejidad
del problema.
- Corto: es el tiempo mínimo para resolver el problema.
- Medio: se estima un tiempo intermedio para contestar el problema.
- Largo: es el tiempo máximo para resolver el problema.
-
Aciertos: resultado de la respuesta del problema, en esta variable solo se considera verdadero o falso (dependiendo de la respuesta).
- Bajo: cuando el problema lo contestó de manera incorrecta.
- Alto: cuando el problema lo contestó de manera correcta.
2. Variables de salida
-
Nivel: es el resultado final de cada misión y se establece con base en el tiempo y el resultado de la respuesta.
- Regresa: regresa al nivel anterior, deshabilitando el nivel en el que el usuario se encuentra (excepto para el nivel uno).
- Mismo: se queda en el mismo nivel, por lo que no genera ninguna acción.
- Siguiente: significa que se desbloquea el siguiente nivel para el mismo subtema en el que se encuentra el estudiante (excepto para el nivel tres).
Para la información de la variable del tiempo del FIS, se diseñó un sitio web el cual contiene todos los problemas que se encuentran en la BD, separados por temas, subtemas y niveles, con el propósito de recopilar y analizar los tiempos en que los estudiantes contestaban cada uno de los problemas, este sitio web contiene un control de los estudiantes que ingresan y responden, los cuales solamente pueden contestar una vez cada uno de los problemas, esto con el propósito de no alterar los tiempos ya sea porque ya conocen el problema o lo realizaron con más tranquilidad fuera del sitio web, asimismo en caso de no encontrar su solución pueden reportarlo, explicando su motivo.
Para la recopilación de los tiempos, se obtuvo la participación de 307 estudiantes del último semestre (sexto) de la Escuela Industrial y Preparatoria Técnica Álvaro Obregón Unidad Tres Caminos, se obtuvo un total de 7,098 respuestas para cada uno de los problemas de la BD, las cuales se dividieron en tres listas:
- Problemas contestados correctamente.
- Problemas contestados de manera incorrecta.
- Problemas reportados (se almacena el motivo por el que se reportó).
Para los problemas reportados se analizaron 105 reportes, de los que se modificaron o restructuraron 10 en total (ya sea en sus respuestas o en la descripción del problema), así como también se eliminaron los valores atípicos de las dos principales listas (los problemas contestados de manera correcta e incorrecta) usando pruebas Grubbs con el paquete estadístico R, para posteriormente comparar si ambas listas son estadísticamente similares con el propósito de determinar el valor mínimo y máximo para la variable de tiempo del FIS con base en la lista de los tiempos contestados de manera correcta o también la de las respuestas incorrectas (en caso de ser ambas listas estadísticamente similares). Asimismo, se establecieron seis reglas difusas para el FIS, como se muestra en la tabla 4.
| Respuesta | Tiempo | ||
| Corto | Medio | Largo | |
| Incorrecta | Retrocede | Retrocede | Retrocede |
| Correcta | Siguiente | Siguiente | Igual |
Cada problema que conforma una misión (cinco problemas en total) es evaluado, por lo que al resultado se le asigna un valor de -1 si regresa, 0 si se queda igual y 1 si avanza al siguiente nivel, se determinaron 21 casos posibles, como se muestra en la tabla 5 sin importar el orden de las respuestas.
| R1 | R2 | R3 | R4 | R5 | Siguiente | Regresa | Igual | Resultado | R | Resultado escrito |
| + | + | + | + | + | 5 | 0 | 0 | 5 | + | Siguiente |
| + | + | + | + | - | 4 | 1 | 0 | 3 | + | Siguiente |
| + | + | + | - | - | 3 | 2 | 0 | 1 | + | Igual |
| + | + | - | - | - | 2 | 3 | 0 | -1 | + | Retrocede |
| + | - | - | - | - | 1 | 4 | 0 | -3 | + | Retrocede |
| - | - | - | - | - | 0 | 5 | 0 | -5 | - | Retrocede |
| + | + | + | + | = | 4 | 0 | 0 | 4 | + | Siguiente |
| + | + | + | = | = | 3 | 0 | 0 | 3 | + | Siguiente |
| + | + | = | = | = | 2 | 0 | 0 | 2 | + | Siguiente |
| + | = | = | = | = | 1 | 0 | 0 | 1 | + | Igual |
| = | = | = | = | = | 0 | 0 | 0 | 0 | = | Igual |
| = | = | = | = | - | 0 | 1 | 0 | -1 | = | Retrocede |
| = | = | = | - | - | 0 | 2 | 0 | -2 | = | Retrocede |
| = | = | - | - | - | 0 | 3 | 0 | -3 | = | Retrocede |
| = | - | - | - | - | 0 | 4 | 0 | -4 | = | Retrocede |
| + | = | - | - | - | 1 | 3 | 0 | -2 | + | Retrocede |
| + | = | = | - | - | 1 | 2 | 0 | -1 | + | Retrocede |
| + | = | = | = | - | 1 | 1 | 0 | 0 | + | Igual |
| + | + | = | = | - | 2 | 1 | 0 | 1 | + | Igual |
| + | + | + | = | - | 3 | 1 | 0 | 2 | + | Siguiente |
| + | + | - | - | = | 2 | 2 | 0 | 0 | + | Igual |
Como se puede observar en la tabla 5, si el total de la suma de los cinco problemas es -1 el estudiante retrocede de nivel, si es 0 o 1 se queda en el mismo y si es mayor a 2 entonces avanza al siguiente nivel de dificultad, como se muestra en la figura 4, la estructura del FIS.
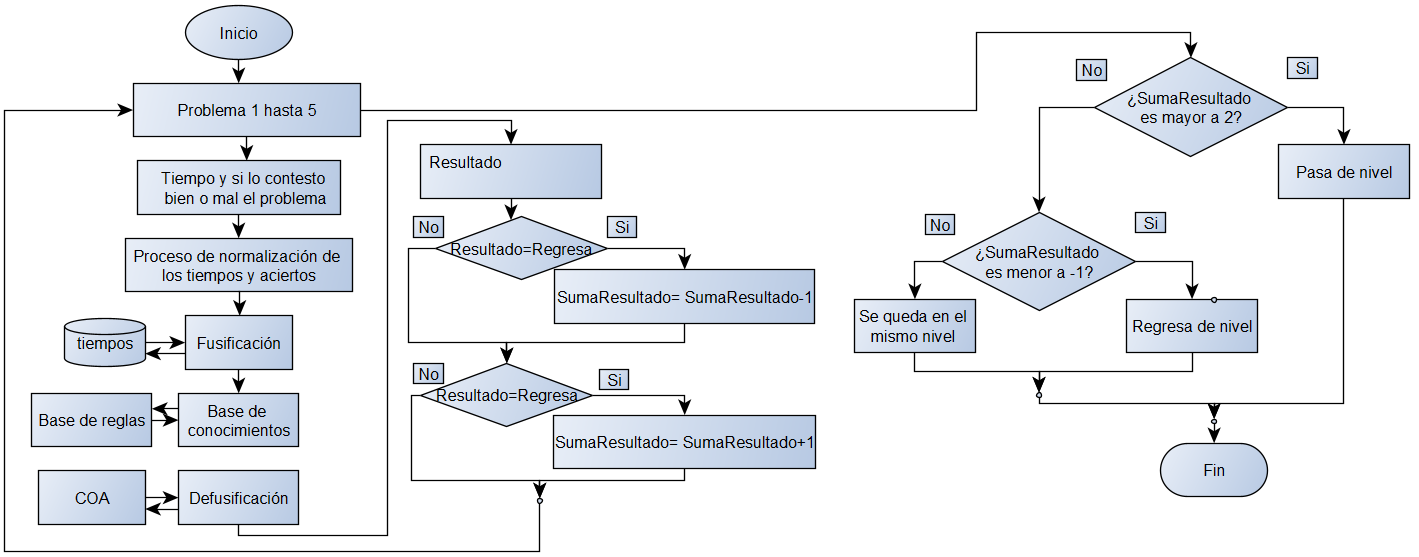
EVALUACIÓN DE APRENDIZAJE
Para el proceso de evaluación del aprendizaje por parte de los estudiantes, se tomó como base la siguiente estructura:
- 1. Se aplica la primera evaluación a los estudiantes.
- 2. Se instala el juego serio y se revisa su correcta instalación y funcionamiento.
- 3. Cuando un usuario entra al juego serio, se almacena en una BD el tiempo invertido, los problemas contestados, sus respuestas, el subtema y el nivel en que se encuentran.
- 4. Se aplica la segunda evaluación con una diferencia de dos semanas después de la instalación del juego serio y la primera evaluación.
- 5. Se analizan los resultados de las evaluaciones con base en la información de la etapa 3, usando pruebas estadísticas de Welch.
Para el paso 1, se desarrollaron dos exámenes con el mismo tema, subtema, nivel y tiempo máximo en contestar con base en la información almacenada en la BD de los problemas que conforman el juego serio, es decir se consideraron problemas similares con base en su complejidad y tiempo máximo de respuesta para cada uno de ellos, posteriormente se reestructuraron con el apoyo de los tres expertos en el área de matemáticas, logrando así que cada uno de los problemas no sea el mismo que se encuentra en la BD del juego serio.
En total, las evaluaciones constan de 30 reactivos de opción múltiple (un problema para cada subtema y nivel) con 30 respuestas correctas y 90 incorrectas, estableciendo un tiempo máximo estimado en contestar de 29:28 minutos para el primer examen y 29:42 para el segundo, el tiempo en el que el estudiante tardó en contestar cada evaluación fue registrado.
Para el paso 3 se desarrolló otra BD con la información de cada uno de los problemas con sus cuatro soluciones y el tiempo máximo de respuesta para la variable del FIS, con el propósito de que al momento que el usuario conteste una misión del juego se guarde en la BD su respuesta y el tiempo invertido de cada problema, el resultado final de cada misión y sus niveles logrados usando la clave de su smartphone (UUID, Universally Unique Identifier) ( Triebel et al., 2018).
Para las pruebas estadísticas se utilizaron las pruebas del paso 4, con el propósito de identificar si existe una diferencia significativa entre los resultados de la primera y segunda evaluación, tomando como base las siguientes hipótesis:
- H0: Los estudiantes mejoraron en la segunda evaluación.
- H1: Los estudiantes no mejoraron en la segunda evaluación.
Participantes
Participaron en total 33 alumnos para el proceso de evaluación, pertenecientes a la Escuela Industrial y Preparatoria Técnica Álvaro Obregón Unidad Tres Caminos de la Universidad Autónoma de Nuevo León en México:
- Todos los estudiantes son de nivel medio superior.
- Llevaron las materias de matemáticas que contienen los conocimientos básicos de aritmética, algebra y estadística.
- Se encuentran a un semestre de entrar a la universidad, es decir están en su último semestre de preparatoria (sexto semestre).
Pruebas de la evaluación de aprendizaje
En total se obtuvieron 8,870 problemas contestados y almacenados en la BD y 66 pruebas (33 aplicados por primera vez y 33 por segunda vez) por parte de los alumnos, para posteriormente ser analizadas como se muestra en las tablas 6 y 7, el número de estudiantes con su respectivo promedio de los resultados y el tiempo para contestar las evaluaciones con base en el tiempo invertido en el juego serio.
| Tiempo (minutos) | # Personas | Primera evaluación | Segunda evaluación |
| 0 | 3 | 66 | 60 |
| 0-30 | 8 | 51 | 55 |
| 30-60 | 6 | 56 | 56 |
| 60-90 | 8 | 52 | 56 |
| 90-120 | 5 | 57 | 67 |
| 120-150 | 2 | 48 | 53 |
| 150-180 | 1 | 47 | 60 |
En la tabla 6 se puede apreciar que los estudiantes que utilizaron el juego serio obtuvieron un promedio general de 52 en la primera evaluación aumentando a 58 en la segunda, a diferencia de los alumnos que no la utilizaron (tiempo 0), los cuales obtuvieron un promedio de 66 a 60 respectivamente.
| Tiempo(minutos) | # Personas | Primera evaluación | Segunda evaluación |
| 0 | 3 | 37 | 26 |
| 0-30 | 8 | 30 | 21 |
| 30-60 | 6 | 30 | 22 |
| 60-90 | 8 | 40 | 25 |
| 90-120 | 5 | 35 | 25 |
| 120-150 | 2 | 41 | 27 |
| 150-180 | 1 | 29 | 26 |
Como se puede observar en la tabla 7, se encontró que los alumnos que usaron el juego obtuvieron un promedio con respecto al tiempo de 34 minutos en la primera y 24 minutos en la segunda evaluación, asimismo para los que no lo utilizaron en ningún momento obtuvieron un promedio de 37 minutos en la primera y 26 minutos en la segunda evaluación; sin embargo, aunque todos los estudiantes disminuyeran su tiempo de respuesta, los estudiantes que no usaron el juego también disminuyeron su promedio general. Para observar los datos desde otra perspectiva se desglosó el porcentaje de estudiantes que avanzaron de nivel con respecto al subtema en el que se encuentran, como se muestra en la tabla 8.
| Subtema | Nivel 1 | % Nivel 1 | Nivel 2 | % Nivel 2 | Nivel 3 | % Nivel 3 |
| Jerarquía de operaciones básicas | 28 | 93% | 27 | 90% | 14 | 47% |
| Relaciones de proporcionalidad | 24 | 80% | 24 | 80% | 21 | 70% |
| Expresiones algebraicas | 24 | 80% | 16 | 53% | 10 | 33% |
| Productos notables | 20 | 67% | 15 | 50% | 9 | 30% |
| Ecuaciones | 14 | 47% | 10 | 33% | 4 | 13% |
| Sistemas de ecuaciones | 11 | 37% | 10 | 33% | 6 | 20% |
| Representaciones gráficas | 12 | 40% | 8 | 27% | 4 | 13% |
| Frecuencias e información gráfica | 21 | 70% | 15 | 50% | 7 | 23% |
| Medidas descriptivas | 14 | 47% | 12 | 40% | 7 | 23% |
| Nociones de probabilidad | 13 | 43% | 10 | 33% | 7 | 23% |
La mayoría de los estudiantes ingresaron al tema de razonamiento aritmético, con un 90% en el subtema de jerarquía de operaciones y un 80% en relaciones de proporcionalidad, después al tema de razonamiento algebraico, con un 80% en expresiones algebraicas y un 67% en productos, por último, al razonamiento estadístico y probabilístico con un 70% en frecuencias e información gráfica.
Asimismo, se observó que el número de estudiantes al pasar al siguiente nivel disminuye, es decir, la mayoría de los estudiantes saben hacer procedimientos lineales directamente (pasar al nivel 2), pero se les complica hacer múltiples procedimientos (pasar nivel 3) o formular modelos a través de análisis usando lenguaje simbólico (completar el nivel 3).
A pesar de que los alumnos llegaron al nivel 3 no significa que lo hayan completado, por lo que se separó el número de subtemas terminados, como se muestra en la tabla 9, los promedios de la primera y la segunda evaluación con respecto al número de subtemas terminados (completando el nivel 3).
| # | Subtemas terminados | # Personas | % Personas | Primera evaluación | Segunda evaluación |
| 1 | 0 | 13 | 39% | 53 | 56 |
| 2 | 1-2 | 13 | 39% | 52 | 58 |
| 3 | 3-4 | 2 | 6% | 48 | 60 |
| 4 | 5-6 | 2 | 6% | 67 | 59 |
| 5 | 7-8 | 3 | 9% | 60 | 61 |
| 6 | 9-10 | 0 | 0% | NA | NA |
Como se puede apreciar en la tabla 9, el 78% de los alumnos completaron dos, uno o ningún subtema, asimismo se analizó la situación de la fila cuatro y se encontró que uno de los dos alumnos se enfocó solamente en cinco subtemas (por lo que no contestó ningún problema de otro subtema), motivo por el que se realizó la tabla 10, en donde se puede observar el número de estudiantes que avanzaron por lo menos al siguiente nivel.
| Avanzó Nivel | # Personas | % Personas | Primera evaluación | Segunda evaluación |
| 0 | 4 | 12% | 63 | 59 |
| 1-2 | 8 | 24% | 45 | 52 |
| 3-4 | 5 | 15% | 61 | 61 |
| 5-6 | 4 | 12% | 57 | 62 |
| 7-8 | 7 | 21% | 47 | 57 |
| 9-10 | 5 | 15% | 60 | 61 |
Para obtener una mejor visualización de los datos, se realizó una gráfica para comparar los promedios de las dos evaluaciones con base en el número de subtemas que los estudiantes lograron avanzar como mínimo al siguiente nivel, como se muestra en la figura 5.
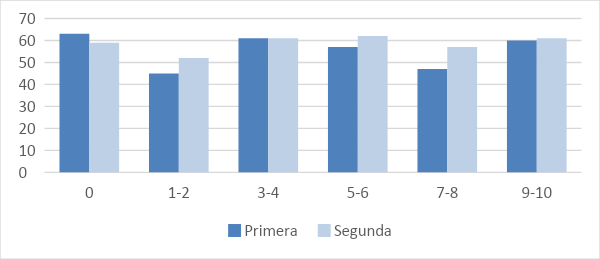
Como se puede observar en la tabla 8 y en la figura 5, los estudiantes que no avanzaron en ninguno de los subtemas disminuyeron su promedio obteniendo una calificación de 63 en la primera evaluación y 59 en la segunda, a diferencia de los que avanzaron por lo menos al siguiente nivel. Con el propósito de conocer si existe evidencia estadística de que los estudiantes mejoraron, se realizaron pruebas de hipótesis usando pruebas Welch para la tabla 10, como se puede apreciar en la tabla 11 (no se realizaron pruebas de hipótesis en las tablas anteriores ya que no se puede determinar una conclusión debido a que en algunos casos el número de muestras es de dos o tres valores).
| Avanzó de nivel | # Personas | Grados de libertad | t |
| 0 | 4 | 5 | 0.741941 |
| 1-2 | 8 | 12 | -1.30926 |
| 3-4 | 5 | 7 | -0.0282843 |
| 5-6 | 4 | 6 | -0.874855 |
| 7-8 | 7 | 12 | -1.41796 |
| 9-10 | 5 | 8 | -0.151411 |
En la tabla 11 se puede apreciar que existe evidencia estadística con un 95% de probabilidad de que los estudiantes que usaron el juego serio mejoraron (t 0 < -ta) a diferencia de los estudiantes que no la usaron (t0 > ta).
Con los resultados observados anteriormente se determinó que, de los 33 estudiantes, 15 de ellos los cuales usaron el juego serio mejoraron, 7 se encuentran en el mismo promedio y el resto disminuyó ya sea porque solo se enfocaron en ciertos subtemas o no utilizaron el juego serio, por lo que se realizaron pruebas de hipótesis como se muestra en la tabla 12 para demostrar que existe evidencia estadística de lo mencionado anteriormente.
| # Personas | Grados de libertad | t | |
| Mejoraron | 15 | 27 | -4.16856 |
| Igual | 7 | NA | NA |
| Empeoraron | 11 | 17 | 2.74829 |
En la tabla 12 se puede apreciar que existe evidencia estadística de que, de los 33 alumnos, 15 mejoraron y 11 empeoraron ya sea porque no le dedicaron suficiente tiempo o simplemente no lo utilizaron con lo que se demuestra que el juego serio ayuda a fortalecer el razonamiento con base en la comparación de las dos evaluaciones.
CONCLUSIÓN
El juego serio tiene como propósito el contribuir a fortalecer el razonamiento lógico matemático de los estudiantes a través de la solución de problemas de matemáticas mientras se divierten, por lo que no aspira a “aprender conceptos” del área, sino más bien a que el estudiante razone el cómo resolver un problema solamente con la información proporcionada. En este juego no existe una manera lineal para jugarlo, por lo que el estudiante puede entrar con toda libertad a cualquiera de los temas y seleccionar un subtema (siempre y cuando se encuentre desbloqueado), obteniendo un resultado final con base en el tiempo y el resultado de la respuesta (si es correcta o incorrecta).
Tomando como base los resultados de la sección anterior, se determinó que entre más tiempo le dediquen y logren avanzar los niveles del juego serio su razonamiento lógico matemático se fortalece, a diferencia de los que no la utilizan. Además, se encontró que no todos los estudiantes que contestaban algún subtema avanzaban de nivel, incluso en algunas ocasiones los alumnos regresaban de nivel en alguno de los subtemas, por lo que se determinó de que el FIS se implementó de manera correcta, como se muestra en las tablas 8 y 9 los estudiantes que avanzaron al menos al siguiente nivel (nivel 2) sí mejoraron en la segunda evaluación a diferencia de los que no la utilizaron o no avanzaron de nivel con base en observación y análisis, así como también a través de evidencia estadística usando una probabilidad del 95%.
Como trabajo futuro se contempla desarrollar los otros dos temas de la guía EXANI-II los cuales consisten en puntos, segmentos, y línea recta (razonamiento geométrico), así como también funciones trigonométricas (razonamiento trigonométrico), con el propósito de obtener un juego que conforme la guía completa del examen de ingreso al nivel superior, asimismo aumentar el tamaño de muestra de los estudiantes que utilicen el juego por más tiempo (mínimo 4 meses), logrando así analizar y conocer si es posible mejorar el razonamiento lógico-matemático a través de un uso prolongado.
REFERENCIAS
Aishah, N., y Syed, S. S. (2014). Sensitivity analysis of Welch’s t-test. 21st National Symposium on Mathematical Sciences (SKSM), (1), 888-893. https://doi.org/10.1063/1.4887707
Alvarez, J., y Djaouti, D. (2011). An introduction to Serious Game-Definitions and concepts. Serious Games & Simulation for Risks Management, 11(1), 11-15.
Armstrong, T. (2006). Inteligencias múltiples en el aula: Guía práctica para educadores. Ediciones Paidós Ibérica, S.A.
Bragdon, A., y Fellows, L. (2003). Juegos de mente. Random House Espanha.
Brezovszky, B., McMullen, J., Veermans, K., Hannula, M., Rodríguez, G., Pongsakdi, N., y Laakkonen, E. (2019). Effects of a mathematics game-based learning environment on primary school students' adaptive number knowledge. Computers & Education, 128(1), 63-74. https://doi.org/10.1016/j.compedu.2018.09.011
CENEVAL (2018). Guía EXANI II. CENEVAL. http://www.ceneval.edu.mx/documents/20182/98406/Guia+EXANI-II+23a+ed.pdf/e1ff950b-2b89-4544-af4b-d5f456fa3ee8
Delacre, M., Lakens, D., y Leys, C. (2017). Why Psychologists Should by Default Use Welch’s t-test. International Review of Social Psychology, 30(1), 92-101. http://doi.org/10.5334/irsp.82
EvolMind (2020). La plataforma Elearning que simplifica la formación online. evolCampus. https://www.evolcampus.com/latam
Fernández, A. (2014). La evaluación de los aprendizajes en la universidad: nuevos enfoques. Publicaciones Universidad Politécnica de Valencia.
García, R. I., Cuevas, O., Vales, J. J., y Cruz, I. R. (2012). Impacto del Programa de Tutoría en el desempeño académico de los alumnos del Instituto Tecnológico de Sonora. Revista Electrónica de Investigación Educativa, 14(1), 106-121.
Gardner, H., y Hatch, T. (1989). Multiple Intelligences Go to School: Educational Implications of the Theory of Multiple Intelligences. Educational Researcher, 18(8), 4-10. http://doi.org/10.2307/1176460
Holvikivi, J. (2007). Logical Reasoning Ability in Engineering Students: A Case Study. IEEE Transactions on Education, 50(4), 367-372. https://doi.org/10.1109/TE.2007.906600
Hurtado, P., García, M., Rivera, D., y Forgiony, J. (2018). Las estrategias de aprendizaje y la creatividad: una relación que favorece el procesamiento de la información. Espacios, 39(17), 1-18.
Huxham, M., Campbell, F., y Westwood, J. (2010). Oral versus written assessments: a test of student performance and attitudes. Assessment & Evaluation in Higher Education, (1), 1-12. https://doi.org/10.1080/02602938.2010.515012
Ibarra, M. J., Soto, W., Ataucusi, P., y Ataucusi, E. (2016). MathFraction: Educational Serious Game for Students Motivation for math learning. XI Latin American Conference on Learning Objects and Technology (LACLO), (1), (pp. 1-9). https://doi.org/10.1109/LACLO.2016.7751777
INEE. (2019a). Planea. INEE. https://www.inee.edu.mx/wp-content/uploads/2019/07/Resultados2017.pdf
INEE. (2019b). SIRE- Sistema Integral de Resultados de las Evaluaciones. INEE. https://www.inee.edu.mx/bases-de-datos-inee-2019/
Jarero, M., Aparicio, E., y Sosa, L. (2013). Pruebas escritas como estrategia de evaluación de aprendizajes matemáticos. Un estudio de caso a nivel superior. Revista latinoamericana de investigación en matemática educativa, (1), 213-243. https://dx.doi.org/10.12802/relime.13.1623
Johnson, P., Khemlani, S. S., y Goodwin, G. P. (2015). Logic, probability, and human reasoning. Trends in Cognitive Sciences, 19(4), 201-214. https://doi.org/10.1016/j.tics.2015.02.006
Kramarski, B., y Mevarech, Z. R. (2003). Enhancing Mathematical Reasoning in the Classroom: The Effects of Cooperative Learning and Metacognitive Training. American Educational Research Journal, 40(1), 281-310. https://doi.org/10.3102/00028312040001281
Larrazolo, N., Backhoff, E., y Tirado, F. (2013). Habilidades de razonamiento matemático de estudiantes de educación media superior en México. Revista mexicana de investigación educativa, 18(59), 1137-1163.
Lasso, N., y Córdoba, J. C. (2015). Evaluación del desempeño de los estudiantes en evaluaciones orales y escritas. Docencia Universitaria, (1), 33-41.
Lithner, J. (2000). Mathematical Reasoning in School Tasks. Educational Studies in Mathematics, 41(2), 165-190. https://doi.org/10.1023/A:1003956417456
López, A. Y. (2020). Desarrollo de un juego serio para fortalecer el razonamiento lógico-matemático con implementación de un sistema basado en lógica difusa (tesis doctoral). Universidad Autónoma de Nuevo León.
López, R. (2017). Origen y evolución del Ceneval. Centro Nacional de Evaluación para la Educación Superior.
Mangowal, R. G., Yuhana, U., Yuniarno, E., y Purnomo, M. (2017). MathBharata: A serious game for motivating disabled students to study mathematics. IEEE 5th International Conference on Serious Games and Applications for Health (SeGAH), (1), 1-6. https://doi.org/10.1109/SeGAH.2017.7939277
Michael, D., y Chen, S. (2006). Serious Games: games that educate, train and inform. Thomson.
Moodle (2020). Empezar es fácil. moodle. https://moodle.org/
OECD. (2018). Programa para la evaluación internacional de alumnos (PISA). OCDE. http://www.oecd.org/pisa/publications/PISA2018_CN_MEX_Spanish.pdf
Quintero, L., Suárez, Y., García, G., y Vanegas, J. (2012). Niveles de pensamiento y resolución de problemas matemáticos en los estudiantes del programa psicología de una universidad pública de Santa Marta (Magdalena). Duazary. Revista Internacional de Ciencias de la Salud, 9(2), 123-131.
Reyes, S., Castillo, A., Zúñiga, A., y Llarena, R. (2012). Niveles de dominio en Habilidad matemática: La estrategia de evaluación de ENLACE Media Superior Marcos de referencia 5. CENEVAL.
Rodríguez, O., Mendivil, G., Arámburo, D., y Valenzuela, D. (2017). Importancia de la aplicación de retos matemáticos para el desarrollo del pensamiento matemático en estudiantes de secundaria. Investigación e Innovación en Matemática Educativa, 2(2), 216-224.
Santibáñez, T. (2016). Manual para la evaluación del aprendizaje estudiantil. Trillas.
Soares, M. A., Gonçalves, T. D., Monteiro, L. F., Machado, A., y Jusan, D. (2016). A Fuzzy Logic Application in Virtual Education. Procedia Computer Science, 91(1), 19-26. https://doi.org/10.1016/j.procs.2016.07.037
Soto, R. I. (2018). Principios que consideran los catedráticos al elaborar problemas matemáticos. UCV - SCIENTIA, 10(2), 132-137. https://doi.org/10.18050/RevUcv-Scientia.v10n2a2
Structuralia (2020). Impulsa tu carrera profesional. Soluciones integrales de formación y gestión structuralia, S. A.http://www.structuralia.com/es/
Triebel, D., Reichert, W., Bosert, S., Feulner, M., Okach, D., Slimani, A., y Rambold, G. (2018). A generic workflow for effective sampling of environmental vouchers with UUID assignment and image processing. Database, (1), 1-10. https://doi.org/10.1093/database/bax096
Notas de autor
E-mail: alicia.lopezsn@uanl.edu.mx
E-mail: aida.gonzalezlr@uanl.edu.mx