Monográfico
Evaluación del resultado académico de los estudiantes a partir del análisis del uso de los Sistemas de Control de Versiones
Evaluation of students’ academic results through the analysis of their use of Version Control Systems
Evaluación del resultado académico de los estudiantes a partir del análisis del uso de los Sistemas de Control de Versiones
RIED. Revista Iberoamericana de Educación a Distancia, vol. 23, núm. 2, 2020
Asociación Iberoamericana de Educación Superior a Distancia
Cómo referenciar este artículo: Gutiérrez Fernández, A., Guerrero Higueras, A. M., Conde González, M. A., y Fernández Llamas, C. (2020). Evaluación del resultado académico de los estudiantes a partir
del análisis del uso de los Sistemas de Control de Versiones. RIED. Revista Iberoamericana de Educación a Distancia, 23(2), pp. 127-145. doi: http://dx.doi.org/10.5944/ried.23.2.26539
Resumen: Una de las herramientas más utilizadas por los profesionales de las tecnologías de la información y la comunicación son los sistemas de control de versiones. Estas herramientas permiten, entre otras cosas, monitorizar la actividad de las personas que trabajan en un proyecto. Por tanto, es recomendable que se utilicen también en las instituciones educativas. El objetivo de este trabajo es evaluar si el resultado académico de los estudiantes se puede predecir monitorizando su actividad en uno de estos sistemas. Para tal efecto, hemos construido un modelo que predice el resultado de los estudiantes en una práctica de la asignatura Ampliación de Sistemas Operativos, perteneciente al segundo curso del grado en Ingeniería Informática de la Universidad de León. Para obtener la predicción, el modelo analiza la interacción del estudiante con un repositorio Git. Para diseñar el modelo, se evalúan varios modelos de clasificación y predicción utilizando la herramienta MoEv. Esta herramienta permite entrenar y validar diferentes modelos de clasificación y obtener el más adecuado para un problema concreto. Además, la herramienta permite identificar las características más discriminantes dentro de los datos de entrada. El modelo resultante ha sido entrenado utilizando los resultados del curso 2016 – 2017. Posteriormente, para asegurar que el modelo generaliza correctamente, se ha validado utilizando datos del curso 2017 – 2018. Los resultados concluyen que el modelo predice el éxito de los estudiantes con un alto porcentaje de acierto.
Palabras clave: aplicación informática, tratamiento de la información, inteligencia artificial, proceso de aprendizaje.
Abstract: Version Control Systems are commonly used by Information and Communication Technology professionals. These systems allow for monitoring programmers' activity working in a project. Thus, the usage of such systems should be encouraged by educational institutions. The aim of this work is to evaluate if students’ academic success can be predicted by monitoring their interaction with a Version Control System. In order to do so, we have built a model that predicts students’ results in a specific practical assignment of the Operating Systems Extension subject. A second-year subject in the degree in Computer Science at the University of León. In order to obtain a prediction, the model analyzes students’ interaction with a Git repository. To build the model, several classifiers and predictors have been evaluated by using the MoEv tool. The tool allows for evaluating several classification and prediction models in order to get the most suitable one for a specific problem. Prior to the model development, Moev performs a feature selection from input data to select the most significant ones. The resulting model has been trained using results from the 2016 – 2017 course year. Later, in order to ensure an optimal generalization, the model has been validated by using results from the 2017 – 2018 course. Results conclude that the model predicts students' outcomes? with a success high percentage.
Keywords: computer application, information processing, machine learning, learning process.
El auge de las Tecnologías de la Información y la Comunicación (TIC) ha cambiado los procesos de enseñanza y aprendizaje. Los docentes utilizan diversas herramientas en sus clases con el objetivo de favorecer el aprendizaje de sus alumnos. Además, los propios alumnos utilizan múltiples aplicaciones tanto en sus centros educativos como fuera de ellos. Sin embargo, ¿es posible afirmar que una herramienta concreta mejora el rendimiento de un estudiante? Si pudiéramos aseverar esto, sería posible utilizar siempre la herramienta que mejor se adapte a una lección o estudiante concretos. Existen muchos estudios sobre el tema, el cual está estrechamente relacionado con las áreas de Learning Analytics y Educational Data Mining.
Learning Analytics se define como la medida, recopilación, análisis y notificación de información relacionada con los estudiantes y su contexto, con el propósito de entender y optimizar el aprendizaje, además del entorno en el que se lleva a cabo (Siemens y Gasevic, 2012). Este campo, junto con el de Educational Data Mining, tiene un alto potencial para entender y optimizar los procesos de enseñanza y aprendizaje. Por ejemplo, el análisis de los datos recopilados por sistemas de información estudiantil (SISs, por sus siglas en inglés), o las interacciones de los estudiantes con sistemas de gestión del aprendizaje (LMSs, por sus siglas en inglés) proporcionan a los docentes una forma de identificar patrones que pueden ser utilizados para predecir resultados o tomar decisiones acerca de la adecuación de los recursos utilizados.
Uno de los problemas más recurrentes en Learning Analytics es la obtención de modelos para predecir los resultados de los alumnos. En concreto, es muy común tratar de calcular el riesgo (probabilidad) de que un estudiante apruebe o suspenda una asignatura (Siemens, Dawson y Lynch, 2013). Este tipo de análisis predictivo tiene una consecuencia importante en educación: nos permite identificar aquellos estudiantes en situación de riesgo. Esta información permite a los profesores llevar a cabo estrategias proactivas que contribuyan a la obtención de un sistema educativo de mayor calidad. Los modelos de predicción a menudo tienen un alto grado de precisión únicamente en escenarios muy concretos (Gašević, Dawson, Rogers y Gasevic, 2016). Esta limitación, aunque esperada debido a que los modelos se calculan mediante algoritmos altamente dependientes de la calidad de los datos, crea dificultades para obtener una visión global del efecto en el éxito académico de ciertas variables, y por tanto, para obtener una herramienta aplicable en diferentes casuísticas.
Uno de los objetivos de este trabajo es presentar Model Evaluator (MoEv), una herramienta que permite evaluar una serie de algoritmos de aprendizaje paramétricos y no paramétricos con el objetivo de elegir el que mejor exactitud (accuracy) presenta ante un problema concreto de predicción. En el caso que nos ocupa, pretendemos conseguir un modelo que permita predecir si los alumnos serán capaces de superar una prueba práctica concreta que, sin embargo, tiene la suficiente relevancia como para considerarse un indicador del éxito académico en la asignatura en la que se realiza. La herramienta, basada en la idea propuesta en Guerrero-Higueras, DeCastro-García y Matellán (2018), se presentó inicialmente en Guerrero-Higueras, DeCastro-García, Matellán y Conde, (2018),y, posteriormente, se extendió en Guerrero-Higueras, DeCastro-García, Rodriguez-Lera, Matellán y Conde Miguel (2019). Se pretende que pueda ser aplicada en diferentes asignaturas o situaciones de aprendizaje y, por tanto, incluye una fase esencial: la selección automática de las variables más discriminantes. Dado que el reto es obtener una herramienta de propósito general, es necesario que las fuentes de datos puedan ser de diferente naturaleza y que la herramienta pueda determinar qué información es más importante para un modelo concreto. Las fuentes de datos más habituales para modelos de predicción en el ámbito educativo son los datos almacenados en SISs ( Kovacic, 2012), en LMSs y similares (Agudo-Peregrina, Iglesias-Pradas, Conde-González y Hernández-García, 2014), o bien en fuentes de datos híbridas a partir de las anteriores (Barber y Sharkey, 2012).
Por otro lado, en algunos campos como la ingeniería o la informática, es muy habitual que los docentes empleen herramientas y aplicaciones avanzadas en sus cursos con el objetivo de brindar a los estudiantes una experiencia de aprendizaje significativa lo más cercana posible del mundo profesional. Por ejemplo, en ingeniería de software, la gestión de cambios en los componentes de un producto software o su configuración se conoce como control de versiones (Fischer, Pinzger y Gall, 2003). Se denomina versión, revisión o edición, al estado del producto en un momento específico. El control de versiones se puede hacer manualmente, aunque es recomendable utilizar alguna herramienta para facilitar esta tarea. Estas herramientas se conocen como sistemas de control de versiones (VCS, por sus siglas en inglés) (Spinellis, 2005). El uso de estas herramientas es una de las habilidades más demandadas en los profesionales de las TIC.
Un VCS debe proporcionar, al menos, las siguientes características: almacenamiento para los diferentes elementos que se han de gestionar, a saber código fuente, imágenes o documentación; mecanismos para la edición de dichos elementos (creación, eliminación, modificación, cambio de nombre, etc.); y registro y etiquetado de todas las acciones realizadas, de tal modo que un elemento pueda regresar a un estado anterior deshaciendo estas acciones. Entre los VCSs más populares están los siguientes: CVS, Subversion (Pilato, Collins-Sussman y Fitzpatrick, 2008) o Git (Torvalds y Hamano, 2010).
El objetivo principal de este trabajo es responder a las siguientes preguntas de investigación:
Pregunta 1: ¿Hay variables que podamos extraer de la interacción de los estudiantes con VCSs que estén relacionadas con el éxito académico?
Pregunta 2: ¿Podemos construir un modelo que permita predecir el éxito de los estudiantes en una tarea, monitorizando la utilización de un VCS?
Para obtener datos que nos permitan responder a las preguntas anteriores, hemos realizado un estudio en el marco de la asignatura Ampliación de Sistemas Operativos del segundo curso del grado en Ingeniería Informática de la Universidad de León. Los resultados preliminares presentados en Guerrero-Higueras, Matellán-Olivera et al. (2018) concluyeron que analizar la actividad de los estudiantes en VCSs permite predecir sus resultados mediante el uso de clasificadores basados en árboles de decisión. Un análisis en profundidad presentado en Guerrero-Higueras, DeCastro-García, Matellán et al. (2018) mostró que los resultados son diferentes dependiendo de las características elegidas. En este último, se sigue el método propuesto en Guerrero-Higueras, DeCastro-García y Matellán (2018) para seleccionar el modelo más adecuado, pero además, se realizó un análisis de variables previo al desarrollo del modelo. En ambos (Guerrero-Higueras, DeCastro-García, Matellán et al., 2018; Guerrero-Higueras, Matellán-Olivera et al., 2018), se utilizó un conjunto de datos de entrenamiento para construir el modelo. Además, para garantizar una generalización óptima, en Guerrero-Higueras, DeCastro-García, Matellán et al., (2018), se realizó una validación del modelo seleccionado utilizando un segundo conjunto de datos. Con respecto a las variables, en Guerrero-Higueras, DeCastro-García, Matellán et al. (2018), se concluyó que considerar algunas variables adicionales a las estrictamente relacionadas con la interacción de los estudiantes con VCS mejora la exactitud de los modelos. Sin embargo, para este trabajo, exploramos los resultados sin agregar ninguna variable externa, lo que a priori garantizaría una generalización óptima y, por tanto, brindaría la posibilidad de utilizar el modelo resultante en diferentes situaciones.
El resto del artículo se organiza de la siguiente forma: la sección “procedimiento experimental” describe la evaluación empírica de los algoritmos de clasificación, los elementos y los métodos utilizados en los experimentos; la sección “resultados” detalla el resultado de la evaluación; la discusión de los resultados se desarrolla en la sección “discusión”; la sección “conclusiones” presenta las conclusiones y las líneas futuras de investigación; por último, se muestran las principales referencias.
PROCEDIMIENTO EXPERIMENTAL
En esta sección se describen todos los elementos utilizados durante el desarrollo y evaluación del modelo de predicción del éxito académico de los estudiantes a partir de su interacción con VCSs. Entre estos elementos se incluyen: una tarea práctica que los estudiantes de Ampliación de Sistemas Operativos (ASO) deben realizar, un VCS para capturar datos, y la herramienta MoEv que permite obtener un modelo optimizado.
Datos de entrada
La asignatura ASO se cursa en el segundo año del Grado en Ingeniería Informática de la Universidad de León y, en ella, se abordan temas relacionados con los sistemas operativos. En concreto, se centra en la gestión interna de la memoria, tanto volátil (memoria RAM) como no volátil (ficheros). También se estudian los problemas relacionados con la seguridad en los sistemas operativos.
La principal tarea práctica que debían superar los estudiantes consistía en implementar un sistema de ficheros basado en i-nodos. Según el enunciado de la práctica, este sistema de ficheros debía funcionar en cualquier distribución Linux, por lo que los estudiantes debían implementar un módulo para el núcleo de Linux (Corbet, Rubini y Kroah-Hartman, 2005) que soporte, como mínimo, las siguientes operaciones: montar dispositivos en el sistema, crear, leer y escribir ficheros; crear nuevos directorios y visualizar el contenido de los directorios existentes.
Se trató de una práctica individual en la que cada estudiante debía utilizar obligatoriamente un VCS para almacenar el código fuente; en concreto, debían usar un repositorio Git. Git sigue un esquema distribuido y, al contrario que otros sistemas que siguen modelos cliente-servidor, cada copia del repositorio incluye el historial completo de los cambios realizados (De Alwis y Sillito, 2009). Se optó por utilizar la plataforma GitHub Classroom (Griffin y Seals, 2013) que permite a los docentes disponer de algunas herramientas de gestión y a los estudiantes trabajar sobre repositorios privados. GitHub es un servicio de almacenamiento basado en la web para proyectos de desarrollo de software que utilizan el sistema de control de versiones Git. Además, GitHub Classroom permite asignar tareas a estudiantes o grupos de estudiantes siempre y cuando se encuentren dentro de la misma organización: en nuestro caso la asignatura ASO.
Con base en la práctica descrita anteriormente se definieron las siguientes variables a extraer de la actividad de los estudiantes en sus respectivos repositorios:
- Identificación anónima del estudiante (id). Utilizado únicamente para diferenciar a los estudiantes.
- Número de operaciones Commit llevadas a cabo por el estudiante (commits).
- Número de días en los que hay, al menos, una operación Commit (days).
- Promedio de operaciones Commit por día (commits/day).
- Número de líneas de código añadidas durante el desarrollo de la práctica (additions).
- Número de líneas de código eliminadas durante el desarrollo de la práctica (deletions).
- En GitHub se llama Issue a los problemas detectados y documentados en un proyecto software para su posterior corrección. La variable issues representa el número de problemas abiertos por los estudiantes.
- La variable closed representa el número de problemas resueltos.
Además de los datos obtenidos de la plataforma GitHub Classroom, se tuvo en cuenta la calificación obtenida por los estudiantes en una prueba llevada a cabo para validar la autoría del código contenido en cada repositorio. Esta prueba de autoría nos permite verificar que los estudiantes han trabajado realmente en el código de sus repositorios. Esta prueba puede tener dos valores: “1” si el estudiante pasa la prueba; “0” si no.
La prueba de autoría es diferente a las variables anteriores ya que no se obtiene directamente de la interacción de los estudiantes con el VCS. En Guerrero-Higueras, DeCastro-García, Matellán et al. (2018) se muestra que esta variable es la más discriminante, aunque en este trabajo de investigación pretendíamos evaluar también los resultados sin tener en consideración la prueba de autoría con el objetivo de asegurar la mejor generalización de los modelos obtenidos.
Se necesitó también una variable objetivo. En nuestro caso, se pretendía determinar si un estudiante finalizó la tarea práctica con éxito o no. Por tanto, en este caso, la variable objetivo es una variable binaria con dos posibles valores: “AP”, para aquellos estudiantes que finalizarán la práctica con éxito; y “SS”, para aquellos que no lo harán.
Los datos obtenidos de la asignatura ASO, en los que se incluyen las características mencionadas anteriormente, proceden de dos grupos de estudiantes. El primer grupo se compone de 46 estudiantes que trataron de realizar la práctica en el curso 2016-2017. Se trata de una muestra balanceada con 21 estudiantes etiquetados como “AP” y 25 estudiantes etiquetados como “SS”. Estos datos se utilizaron para entrenar y validar el modelo de predicción y nos referiremos a ellos como conjunto de datos de entrenamiento.
En el segundo grupo hay 40 estudiantes que trataron de realizar la práctica en el curso 2017-2018, con un total de “AP” y “SS”, de 21 y 19 respectivamente. Estos datos se utilizaron para evaluar la generalización el modelo de predicción y nos referiremos a ellos como conjunto de datos de test.
Diseño del modelo
Para conseguir el mejor modelo de predicción posible, se desarrolló la herramienta MoEv siguiendo el método propuesto en Guerrero-Higueras, DeCastro-García y Matellán (2018). Adicionalmente, se incluyó una fase previa al proceso de selección de variables. En el desarrollo de MoEv se utilizó la librería Scikit-learn (Pedregosa et al., 2011). La figura 1 muestra las distintas etapas de la ejecución de la herramienta.
Se parte de un conjunto de datos que contiene dos tipos diferentes de datos. Por un lado, se consideran variables que provienen directamente de la fuente de datos, e.g. un SIS o un LMS. A estos nos referiremos como datos en bruto. En concreto, las siguientes variables proceden directamente de datos en bruto: id, commits, additions, deletions, issues y closed.
Por otro lado, se consideran variables que un investigador obtiene basándose en los datos en bruto, o que son ofrecidos por otras fuentes de datos como la observación o la actividad cara a cara. A éstos nos referiremos como datos sintéticos. En este caso, las siguientes variables se consideran sintéticas: days, commits/day y prueba de autoría.
Nos referiremos a estas variables en bruto y sintéticas como características (features). Además de estas características, es necesaria una variable objetivo (class) que nos permita entrenar y probar el modelo. Como se ha mencionado anteriormente, nuestra variable objetivo tiene dos posibles valores: “AP” y “SS”.
Como muestra la figura 1, una vez que se dispone del conjunto de datos de entrada, el siguiente paso consistía en determinar cuáles son las variables más significativas para obtener un modelo de clasificación basado en la variable objetivo. La selección de variables es un procedimiento por el cual se seleccionan las variables que más contribuyen a la clasificación o predicción. Realizando esta selección de variables previa a la definición del modelo, es posible conseguir una reducción del sobre-entrenamiento (overfitting), mejorar la exactitud y, obviamente, reducir el tiempo de entrenamiento. Hay varios tipos de métodos de selección de variables, entre otros: selección univariable, eliminación de variables recursivas o cálculo de la importancia mediante algoritmos de aprendizaje. En este caso, debido a la naturaleza del conjunto de datos y a que los datos no siguen una distribución normal, se ha optado por los últimos. Los métodos por conjuntos (ensembles) son una buena opción porque nos permiten elegir el tipo de algoritmo que queremos utilizar.

Los resultados obtenidos en un estudio preliminar (Guerrero-Higueras, Matellán-Olivera et al., 2018) muestran que los algoritmos basados en árboles obtienen un buen resultado procesando nuestro conjunto de datos. Siguiendo el mismo criterio, hemos seleccionado un árbol extremadamente aleatorio ( Geurts, Ernst y Wehenkel, 2006) para realizar la selección de variables. Solamente se seleccionan las variables con una importancia superior a un determinado umbral. La importancia de las variables se calcula mediante el coeficiente Gini (G).
Una vez escogidas las variables más significativas, se aplican varios algoritmos con el fin de predecir la variable objetivo a partir de datos de entrada. Las técnicas de clasificación supervisada se pueden dividir en dos categorías diferentes: modelos paramétricos y no paramétricos. En el primer caso, se dispone de un número fijo y finito de parámetros según el mapa de clasificación. Estos algoritmos de aprendizaje automático pueden ser efectivos porque son sencillos y no necesitan muchos datos de entrenamiento para conseguir un buen rendimiento. Sin embargo, son adecuados únicamente para problemas específicos y pueden ser demasiado limitados en algunas situaciones. Por otro lado, en los algoritmos no paramétricos, el número de parámetros no es conocido y pueden crecer dependiendo del conjunto de datos de entrenamiento. Estos modelos son más flexibles y potentes, pero necesitan más datos de entrenamiento y existe un mayor riesgo de sobre-entrenamiento. Dado que el objetivo del diseño es obtener una herramienta de propósito general, hemos incluido los dos tipos de algoritmos con el objetivo de encajar en la mayor cantidad de situaciones educativas posibles.
Específicamente, MoEv trabaja con los siguientes algoritmos de clasificación y predicción que, a priori, son los más prometedores:
- Adaptive Boosting (AB). Los métodos de conjunto combinan diferentes clasificadores básicos convirtiendo el proceso de aprendizaje en un método más preciso. AB es uno de los métodos de conjunto más populares.
- Árboles de clasificación y regresión (CART, por sus siglas en inglés). Un árbol de decisión es un método que predice la etiqueta asociada a un elemento recorriendo un árbol desde el nodo raíz hasta una hoja (Hastie, Tibshirani y Friedman, 2009). Es un método no paramétrico en el que los árboles crecen desde arriba hacia abajo en un proceso iterativo.
- K-Nearest Neighbors (KNN). Aunque el concepto de los k vecinos más cercanos es el fundamento de muchos métodos de aprendizaje, en su mayoría no supervisado, también permite la clasificación supervisada con variables objetivo. Es una técnica no paramétrica que clasifica nuevas observaciones en base a la distancia con la observación en el conjunto de entrenamiento (Devroye, Györfi y Lugosi, 2013; Duda, Hart y Stork, 2012).
- Análisis discriminante lineal (LDA, por sus siglas en inglés). Método paramétrico que asume que la distribución de los datos es gaussiana multivariante (Duda et al., 2012). LDA asume el conocimiento de parámetros de población o, en caso contrario, se puede utilizar la estimación de máxima verosimilitud. LDA utiliza la aproximación Bayesiana para seleccionar la categoría que maximiza la probabilidad condicional (Bishop, 2006; Koller y Friedman, 2009; Murphy, 2012).
- Regresión logística (LR, por sus siglas en inglés). Los métodos lineales se suelen utilizar en regresiones en las que se espera que el valor objetivo sea una combinación lineal de las variables de entrada. LR, a pesar de su nombre, es un modelo lineal de clasificación y no de regresión. En este modelo, las probabilidades que describen un posible resultado son modeladas utilizando una función logística.
- Perceptrón multicapa (MLP, por sus siglas en inglés). Una red neuronal artificial es un modelo inspirado en la estructura del cerebro humano. Las redes neuronales se utilizan cuando no se conocen el tipo de relaciones entre las entradas y las salidas. La red se organiza en capas (una capa de entrada, una capa de salida, y una o varias capas ocultas). Cada capa consta de una serie de nodos que se organizan en un grafo dirigido en el que cada capa está completamente conectada con la siguiente. Es una modificación del Perceptrón lineal estándar y su mejor característica es que es capaz de distinguir datos que no se pueden separar linealmente. Una MLP utiliza propagación hacia atrás para entrenar la red ( Rumelhart, Hinton y Williams, 1985; Cybenko, 1989).
- Naive Bayes (NB). Este método se basa en aplicar el teorema de Bayes con la suposición ingenua (naive) de independencia entre cada par de características (Zhang, 2004; Duda et al., 2012).
- Árboles de Decisión Aleatorios (RF, por sus siglas en inglés). Este clasificador consiste en una colección de árboles de decisión en la que cada árbol se construye aplicando un algoritmo al conjunto de entrenamiento y un vector aleatorio adicional que se remuestrea utilizando Bootstrapping (Breiman, 2001).
Para el ajuste de los modelos anteriores con el conjunto de datos de entrada, MoEv realiza una validación cruzada con k iteraciones. Tras obtener varios modelos utilizando los algoritmos anteriores, se evaluaron para seleccionar el mejor que se adapta al problema. Para realizar esta tarea, se calcularon algunos indicadores de rendimiento (KPI, por sus siglas en inglés). Uno de ellos es la exactitud (accuracy). La exactitud se calcula como se muestra en la ecuación 1, donde es el número de verdaderos positivos y es el número de verdaderos negativos.
Los tres modelos con exactitud mayor son preseleccionados para una evaluación en profundidad considerando los siguientes KPIs adicionales: precisión, exhaustividad (Recall) y F 1-score; todos los cuales se obtienen a través de la matriz de confusión.
La precisión (P) se calcula como se muestra en la ecuación 2, en la cual es el número de falsos positivos.
La exhaustividad o Recall (R) se calcula como muestra la ecuación 3, en la cual es el número de falsos negativos.
Estas dos cifras están relacionadas con el F1-score, el cual se define como la media armónica de la precisión y la exhaustividad, tal y como se muestra en la ecuación 4.
RESULTADOS
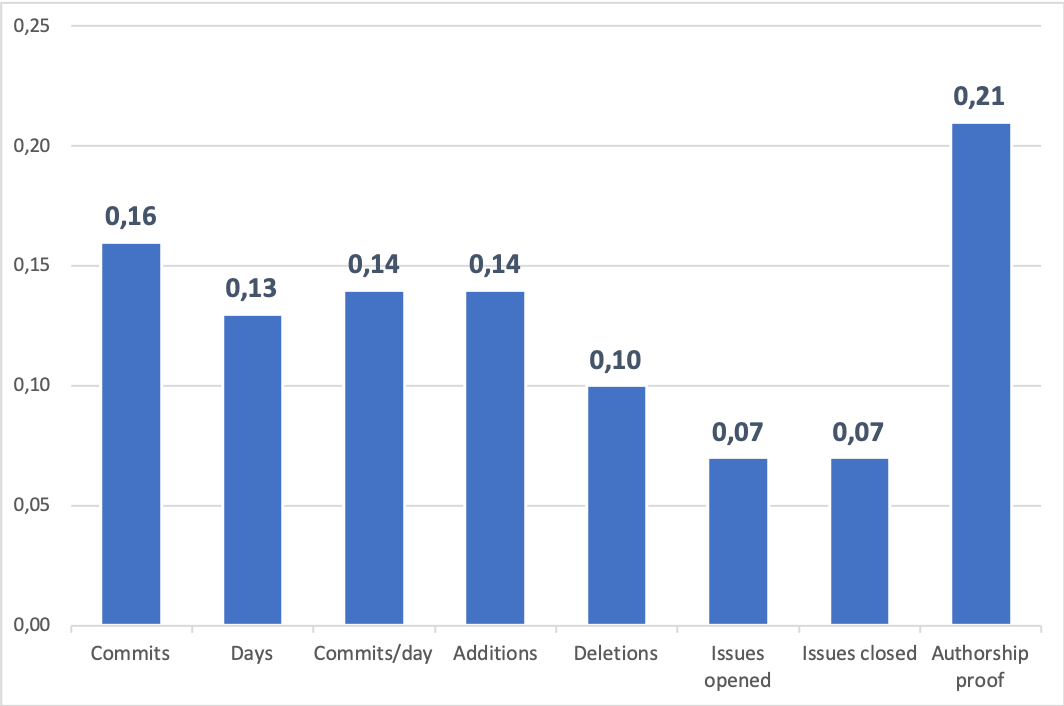
La figura 2 muestra la importancia (peso) de las variables de entrada calculada con el coeficiente Gini tal y como se muestra en Guerrero-Higueras, DeCastro-García, Matellán et al. (2018). Se descartaron las variables con un bajo coeficiente de Gini (G ≤ 0.1). En concreto, las variables seleccionadas fueron las siguientes: prueba de autoría (G = 0.21), commits (G = 0.16), commits/day (G = 0.14), additions (G = 0.14) y days (G = 0.13).
Como se ha mencionado anteriormente, la prueba de autoría es la variable más significativa. En base a esto, la tabla 1 muestra la exactitud (accuracy) utilizando los conjuntos de datos de entrenamiento y test, calculados por la herramienta MoEv en una ejecución con 10 iteraciones. Debido a que la generalización del modelo es esencial, los modelos se han ordenado en base a su accuracy con el conjunto de datos de test. Las puntuaciones más altas con el conjunto de datos de test están remarcadas en negrita.
| NB | RF | LDA | MLP | CART | AB | LR | KNN | |
| Accuracy score (entrenamiento) | 0.8 | 0.8 | 0.8 | 0.5 | 0.4 | 0.4 | 0.7 | 0.6 |
| Accuracy score (test) | 0.8 | 0.8 | 0.7 | 0.7 | 0.6 | 0.5 | 0.5 | 0.5 |
La tabla 2 muestra también la exactitud (accuracy) con los conjuntos de datos de entrenamiento y de test calculada de la misma manera, pero, en este caso, sin tener en cuenta la prueba de autoría.
| RF | MLP | LDA | CART | NB | KNN | AB | LR | |
| Accuracy score (entrenamiento) | 0.7 | 0.4 | 0.6 | 0.6 | 0.5 | 0.6 | 0.4 | 0.6 |
| Accuracy score (test) | 0.7 | 0.7 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 | 0.4 |
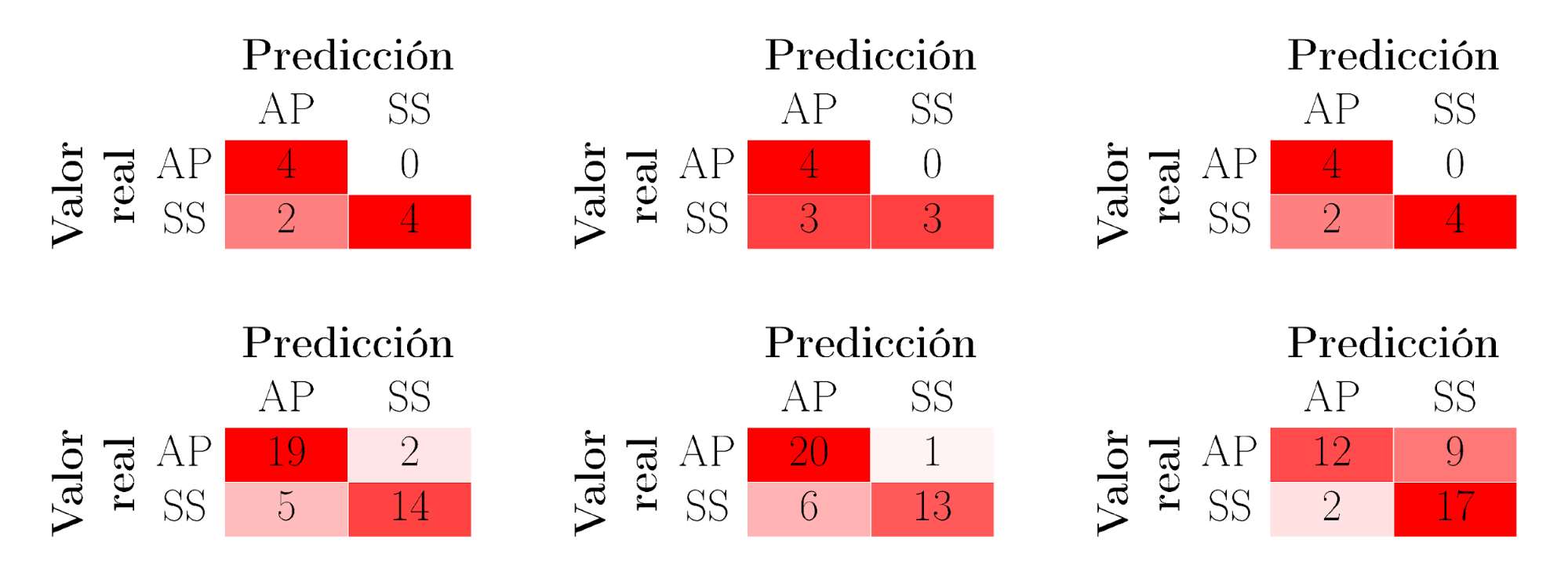
La figura 3, en su parte superior, muestra las matrices de confusión de los modelos resaltados en la tabla 1: NB, RF y LDA; utilizando el conjunto de datos de entrenamiento. En su parte inferior, muestra los mismos datos utilizando el conjunto de datos de test.
La tabla 3 muestra la precisión (P), la exhaustividad o Recall (R) y F1-score con el conjunto de datos de entrenamiento, también para los modelos resaltados en la tabla 1.
| Modelo | NB | RF | LDA | ||||||
| Clase | AP | SS | media | AP | SS | media | AP | SS | media |
| P | 0.67 | 1.00 | 0.87 | 0.67 | 1.00 | 0.87 | 0.67 | 1.00 | 0.87 |
| R | 1.00 | 0.67 | 0.80 | 1.00 | 0.67 | 0.80 | 1.00 | 0.67 | 0.80 |
| F1-score | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 |
| Muestras | 4 | 6 | 10 | 4 | 6 | 10 | 4 | 6 | 10 |
La tabla 4 muestra la precisión (P), la exhaustividad o Recall (R) y F1-score con el conjunto de datos de test, también para los modelos resaltados en la tabla 1.
| Modelo | NB | RF | LDA | ||||||
| Clase | AP | SS | media | AP | SS | media | AP | SS | media |
| P | 0.79 | 0.88 | 0.83 | 0.76 | 0.87 | 0.81 | 0.86 | 0.65 | 0.76 |
| R | 0.90 | 0.74 | 0.82 | 0.90 | 0.68 | 0.80 | 0.57 | 0.89 | 0.72 |
| F1-score | 0.84 | 0.80 | 0.82 | 0.83 | 0.76 | 0.80 | 0.69 | 0.76 | 0.72 |
| Muestras | 21 | 19 | 40 | 21 | 19 | 40 | 21 | 19 | 40 |
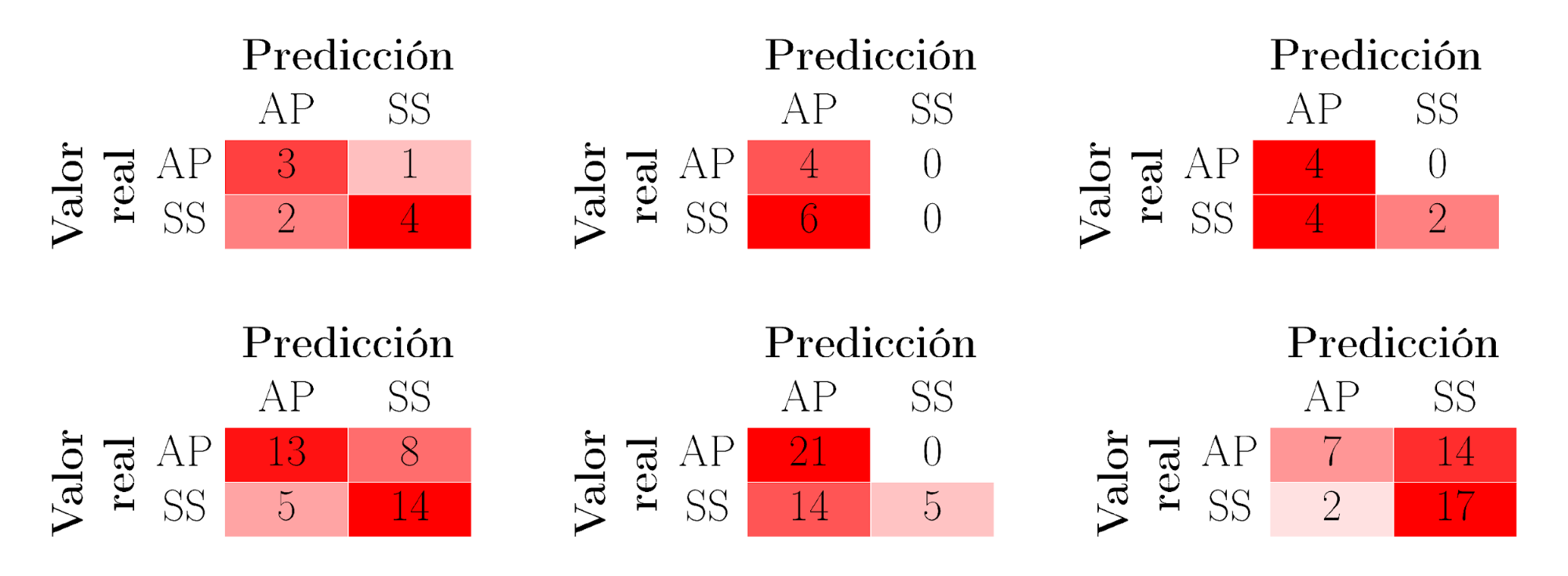
La figura 4, en su parte superior, muestra las matrices de confusión de los modelos resaltados en la tabla 2: RF, MLP y LDA; utilizando el conjunto de datos de entrenamiento sin tener en cuenta la prueba de autoría. En su parte inferior, muestra los mismos datos utilizando el conjunto de datos de test.
La tabla 5 muestra la precisión, la exhaustividad o Recall y F1-score con el conjunto de datos de entrenamiento, también para los modelos seleccionados en la tabla 2, sin tener en cuenta la prueba de autoría. La tabla 6 muestra la precisión, la exhaustividad o Recall y F1-score utilizando el conjunto de datos de test para los modelos resaltados en la tabla 2, sin tener en cuenta la prueba de autoría.
| Modelo | RF | MLP | LDA | ||||||
| Clase | AP | SS | media | AP | SS | media | AP | SS | media |
| P | 0.60 | 0.80 | 0.72 | 0.40 | 0.00 | 0.16 | 0.50 | 1.00 | 0.80 |
| R | 0.75 | 0.77 | 0.70 | 1.00 | 0.00 | 0.40 | 1.00 | 0.33 | 0.60 |
| F1-score | 0.67 | 0.73 | 0.70 | 0.57 | 0.00 | 0.23 | 0.67 | 0.50 | 0.57 |
| Muestras | 4 | 6 | 10 | 4 | 6 | 10 | 4 | 6 | 10 |
| Modelo | RF | MLP | LDA | ||||||
| Clase | AP | SS | media | AP | SS | media | AP | SS | media |
| P | 0.72 | 0.64 | 0.68 | 0.60 | 1.00 | 0.79 | 0.78 | 0.55 | 0.67 |
| R | 0.62 | 0.74 | 0.68 | 1.00 | 0.26 | 0.65 | 0.33 | 0.89 | 0.60 |
| F1-score | 0.67 | 0.68 | 0.67 | 0.75 | 0.42 | 0.57 | 0.47 | 0.68 | 0.57 |
| Muestras | 21 | 19 | 40 | 21 | 19 | 40 | 21 | 19 | 40 |
DISCUSIÓN
La figura 2 muestra el peso de cada una de las variables seleccionadas. Según la figura, la prueba de autoría es la variable más discriminante. Esta prueba permite evaluar el conocimiento que tienen los estudiantes sobre el contenido de sus repositorios. La prueba es importante para verificar que son los propios estudiantes, y nadie más, quienes han trabajado en el repositorio. Por otro lado, es lógico que el hecho de demostrar conocimiento sobre el contenido en sus repositorios tenga un peso importante a la hora de predecir el éxito académico.
En lo que respecta a las otras variables, commits, additions, days y commits/day son las más discriminantes (G > 0.1). Todas ellas son resultado de la interacción de los estudiantes con el VCS, de tal manera que podemos asegurar que la interacción estudiante-VCS está relacionada con el resultado académico. Por otro lado, no existen grandes diferencias entre estas características, por lo que su peso puede cambiar con un conjunto de datos diferente.
La tabla 1 muestra la exactitud calculada por MoEv para los algoritmos descritos anteriormente. Los tres modelos con puntuaciones más altas en el conjunto de datos de test son los que a priori presentan una mejor generalización. En concreto, NB, RF y LDA presentan la exactitud más alta para el conjunto de datos de test. Son también los modelos que presentan una exactitud mayor para el conjunto de datos de entrenamiento. Esto puede ser un indicador de que ambos conjuntos de datos son similares. Sin embargo, para asegurarlo necesitamos verificar que no existen diferencias estadísticamente significativas entre ambos conjuntos de datos. Un análisis similar se ha llevado a cabo en Guerrero-Higueras, DeCastro-García, Rodríguez-Lera y Matellán (2017).
Con los tres modelos anteriores, NB, RF y LDA, se realiza un análisis en profundidad con la información que aportan sus respectivas matrices de confusión para asegurar que generalizan de manera óptima. A este respecto, un elemento importante que debe analizarse es la sensibilidad del modelo para detectar un resultado positivo: por ejemplo, la relación de verdaderos positivos que el modelo clasifica de forma incorrecta. La figura 3, y las tablas 3 y 4 muestran que el modelo NB tiene mejores valores de precisión (P), Recall (R) y F1-score que los modelos RF y LDA, tanto si consideramos el conjunto de datos de entrenamiento, como el de test.
La tabla 2 muestra la exactitud sin tener en cuenta la prueba de autoría. Al igual que en el análisis previo, los modelos con mayor puntuación para el conjunto de datos de test son pre-seleccionados para un análisis en profundidad que asegure una generalización óptima. RF, MLP y LDA tienen mayor exactitud si consideramos el conjunto de datos de test. Estos modelos no son los que obtienen la exactitud más alta para el conjunto de datos de entrenamiento. Con estos tres modelos, se realiza un análisis en profundidad a partir de sus matrices de confusión. La figura 4 así como las tablas 5 y 6 muestran que el modelo RF tiene mejores valores de precisión (P), Recall (R) y F1-score que los modelos MLP y LDA, tanto si consideramos el conjunto de datos de entrenamiento, como el de test.
CONCLUSIONES
Entre las contribuciones principales del trabajo descrito en este artículo, está la propia herramienta MoEv. Permite definir modelos de predicción para diferentes casuísticas llevando a cabo una selección de características como paso previo a la validación cruzada de diferentes algoritmos de clasificación y predicción con el objetivo de seleccionar el que mejor se adapta a unas circunstancias determinadas. En concreto, en este trabajo la herramienta se ha utilizado para diseñar un modelo generalizable que permita predecir el éxito académico monitorizando la actividad de los estudiantes en un VCS.
El artículo plantea también dos preguntas de investigación: ¿Hay características que podamos extraer de la interacción de los estudiantes con VCSs que estén relacionadas con el éxito académico? y, en segundo lugar, ¿Podemos construir un modelo que permita predecir el éxito de los estudiantes en una tarea práctica, monitorizando su uso de un VCS?
Con respecto a la primera pregunta, el análisis de las variables en los datos de entrada permite determinar cuáles son las más relevantes. Esto permite identificar aquellas que tienen un mayor peso en el modelo. Este es el primer paso para obtener un modelo de clasificación que permita predecir el éxito académico de los estudiantes. Los resultados muestran que algunas variables relacionadas con la interacción de los estudiantes con el VCS son discriminantes. Sin embargo, incluir variables adicionales, como la prueba de autoría, aumenta la precisión del modelo.
En lo que respecta a la segunda pregunta, la herramienta MoEv nos ha permitido obtener un modelo de predicción evaluando varios clasificadores. Existe trabajo por hacer en lo relativo al ajuste de los hiper-parámetros para la optimización del modelo seleccionado, pero los resultados son lo suficientemente buenos como para afirmar que podemos predecir el resultado de los estudiantes en una tarea práctica con un alto porcentaje de acierto.
Las líneas futuras de investigación deben afrontar la mejora de la precisión. Para conseguirla, además del ajuste de los hiper-parámetros, sería deseable incrementar el conjunto de datos destinados al entrenamiento de los modelos. Una primera aproximación puede llevarse a cabo combinando los conjuntos de datos de entrenamiento y test. Para ello, es necesario realizar un análisis previo de ambos conjuntos de datos para asegurar que no existen diferencias estadísticamente significativas entre ambos.
REFERENCIAS
Agudo-Peregrina, Á. F., Iglesias-Pradas, S., Conde-González, M. Á., y Hernández-García, Á. (2014). Can we predict success from log data in VLEs? Classification of interactions for learning analytics and their relation with performance in VLE-supported F2F and online learning. Computers in Human Behavior, 31(0), 542-550. http://dx.doi.org/10.1016/j.chb.2013.05.031
Barber, R., y Sharkey, M. (2012). Course correction: using analytics to predict course success. Vancouver, British Columbia, Canada: Association for Computing Machinery.
Bishop, C. M. (2006). Pattern recognition and machine learning. Springer.
Breiman, L. (2001). Random forests. Machine learning, 45(1), 5-32.
Corbet, J., Rubini, A., y Kroah-Hartman, G. (2005). Linux Device Drivers: Where the Kernel Meets the Hardware: "O'Reilly Media, Inc."
Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of control, signals and systems, 2(4), 303-314.
De Alwis, B., y Sillito, J. (2009). Why are software projects moving from centralized to decentralized version control systems? Paper presented at the Proceedings of the 2009 ICSE Workshop on cooperative and human aspects on software engineering.
Devroye, L., Györfi, L., y Lugosi, G. (2013). A probabilistic theory of pattern recognition (Vol. 31): Springer Science & Business Media.
Duda, R. O., Hart, P. E., y Stork, D. G. (2012). Pattern classification: John Wiley & Sons.
Fischer, M., Pinzger, M., y Gall, H. (2003). Populating a Release History Database from Version Control and Bug Tracking Systems. Paper presented at the Proceedings of the International Conference on Software Maintenance.
Gašević, D., Dawson, S., Rogers, T., y Gasevic, D. (2016). Learning analytics should not promote one size fits all: The effects of instructional conditions in predicting academic success. The Internet and Higher Education, 28, 68-84. https://doi.org/10.1016/j.iheduc.2015.10.002
Geurts, P., Ernst, D., y Wehenkel, L. (2006). Extremely randomized trees. Machine learning, 63(1), 3-42.
Griffin, T., y Seals, S. (2013). GitHub in the classroom: not just for group projects (Vol. 28): Consortium for Computing Sciences in Colleges.
Guerrero-Higueras, Á. M., DeCastro-García, N., y Matellán, V. (2018). Detection of Cyber-attacks to indoor real time localization systems for autonomous robots. Robotics and Autonomous Systems, 99, 75-83. https://doi.org/10.1016/j.robot.2017.10.006
Guerrero-Higueras, Á. M., DeCastro-García, N., Matellán, V., y Conde, M. Á. (2018). Predictive models of academic success: a case study with version control systems. Salamanca, Spain: Association for Computing Machinery.
Guerrero-Higueras, Á. M., DeCastro-García, N., Rodríguez-Lera, F. J., y Matellán, V. (2017). Empirical analysis of cyber-attacks to an indoor real time localization system for autonomous robots. Computers & Security, 70, 422-435.
Guerrero-Higueras, Á. M., Matellán-Olivera, V., Costales, G. E., Fernández-Llamas, C., Rodriguez-Sedano, F. J., y Conde, M. Á. (2018). Model for Evaluating Student Performance Through Their Interaction With Version Control Systems. Paper presented at the Proceedings of the Learning Analytics Summer Institute Spain 2018 . León, Spain.
Guerrero-Higueras Ángel, M., DeCastro-García, N., Rodriguez-Lera, Francisco, J., Matellán, V., y Conde Miguel, Á. (2019). Predicting academic success through students’ interaction with Version Control Systems. Open Computer Science, 9(1), 243. https://doi.org/10.1515/comp-2019-0012
Hastie, T., Tibshirani, R., y Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction: Springer Science & Business Media.
Koller, D., y Friedman, N. (2009). Probabilistic graphical models: principles and techniques: MIT press.
Kovacic, Z. (2012). Predicting student success by mining enrolment data. Research in Higher Education Journal, 15, 1-20.
Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective: MIT Press.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., . . . Dubourg, V. (2011). Scikit-learn: Machine learning in Python. Journal of machine learning research, 12(Oct), 2825-2830.
Pilato, C. M., Collins-Sussman, B., y Fitzpatrick, B. W. (2008). Version Control with Subversion: Next Generation Open Source Version Control: " O'Reilly Media, Inc.".
Rumelhart, D. E., Hinton, G. E., y Williams, R. J. (1985). Learning internal representations by error propagation. (No. ICS-8506). California Univ San Diego La Jolla Inst for Cognitive Science.
Siemens, G., Dawson, S., y Lynch, G. (2013). Improving the quality and productivity of the higher education sector. Policy and Strategy for Systems-Level Deployment of Learning Analytics. Canberra, Australia: Society for Learning Analytics Research for the Australian Office for Learning and Teaching.
Siemens, G., y Gasevic, D. (2012). Guest editorial-learning and knowledge analytics. Journal of Educational Technology & Society, 15(3), 1-2.
Spinellis, D. (2005). Version control systems. IEEE Software, 22(5), 108-109.
Torvalds, L., y Hamano, J. (2010). Git: Fast version control system. Recuperado de http://git-scm.com
Zhang, H. (2004). The optimality of naive Bayes. AA, 1(2), 3.
Notas de autor
E-mail: alexis.gutierrez@unileon.es
E-mail: am.guerrero@unileon.es
E-mail: miguel.conde@unileon.es
E-mail: camino.fernandez@unileon.es