1. INTRODUCCIÓN
Las visualizaciones de datos humanísticos requieren de distinciones particulares que las hacen diferentes a las de otros campos del conocimiento. Cuando se trata de estudiar la cultura a través de información y gráficos, puede resultar insuficiente, e incluso problemático, hacer uso exclusivo de estrategias visuales propias de la Estadística, las Ciencias Exactas, las Finanzas, la Geografía u otras disciplinas; especialmente si no se toma una postura reflexiva con respecto a cómo se puede dar cuenta suficiente de los sentidos complejos en los que opera la cultura. Este artículo tiene como finalidad establecer unos fundamentos que permitan una reflexión metódica con respecto a los usos y las estrategias que pueden adoptarse cuando se planea visualizar datos culturales propios de las Humanidades.
Aquí se describirá una serie de estrategias de visualización de datos basada en una famosa clasificación de los signos propuesta por el filósofo y semiólogo Charles S. Peirce: los signos icónicos, los signos indéxicos y los signos simbólicos (1992b). Tales categorías servirán como guía para definir conceptos esenciales para la creación de gráficos de información y para plantear las necesidades particulares de su uso en las Humanidades Digitales. Además, se ofrecerán algunos ejemplos concretos que permitirán ver con mayor claridad los usos, ventajas y desventajas de distintos tipos de visualizaciones, aprovechando el sistema de clasificación propuesto por Peirce.
2. CONCEPTOS FUNDAMENTALES
2.1. Qué entender por visualización de datos
En pocas palabras, podemos decir que la visualización de datos consiste en la creación y posterior lectura de signos visuales, derivados de datos, para construir un argumento o para ayudar al entendimiento de agentes humanos. Las visualizaciones, en este sentido, permiten obtener un insight acerca de un mundo –es decir, un entendimiento generalizado, el establecimiento de conexiones que forman una estructura de pensamiento, la visión completa de las implicaciones de un problema. Las visualizaciones de datos normalmente operan como interfaces, pues sirven como un medio que permite la comunicación entre dos sistemas: el sistema de los datos y el del pensamiento humano (Scolari, 2004). Como los periféricos computacionales que se comunican entre sí –digamos, una impresora con un computador– o los intérpretes que comunican a personas que no hablan el mismo lenguaje, estos procesos gráficos convierten los datos, que pueden o no seguir una lógica computacional, en formas interpretables y entendibles para los humanos.
Los filósofos de la mente Clark y Chalmers (1998) proponen en su Teoría de la mente extendida que los seres humanos usamos, comúnmente, objetos para reemplazar o aumentar parte de nuestra capacidad cognitiva. Por ejemplo, utilizamos anotaciones en libretas para guardar parte de nuestra memoria, teléfonos celulares para comunicarnos a distancia, vehículos para potenciar nuestra capacidad de movimiento. Del mismo modo, empleamos signos visuales para entender mejor un tema, para verlo desde otra escala o perspectiva, o para comunicar un mensaje o un argumento a alguien más. Es en este sentido que los gráficos extienden nuestra mente: potencian nuestra capacidad para pensar y actuar en el mundo; potencian nuestra cognición. Adicionalmente, si adaptamos las ideas de los lingüistas Turner y Fauconnier (2003) a nuestro interés particular, podríamos decir que las visualizaciones de datos ayudan a traer a escala humana lo que opera en rangos espaciotemporales extensos, en escalas cuantitativas inabarcables o en relaciones complejas entre elementos diversos. Por ejemplo, una línea de tiempo puede ayudarnos a traer a escala humana rangos temporales que exceden nuestra experiencia de la vida cotidiana o vital, pues es una compresión de acontecimientos. Un gráfico de barras, a su vez, permite tomar agregados de datos extensísimos y reducirlos a marcas visuales que facilitan la comparación y, en consecuencia, el insight y futuras decisiones. Un grafo posibilita establecer conexiones entre elementos disímiles para así encontrar una estructura compleja, un patrón emergente que no sería evidente si se considera cada elemento aisladamente. La producción computarizada de visualizaciones hace más eficiente y automática la transformación de datos que existen en escalas extensas en gráficos manejables para la cognición de un ser humano.
2.2. La clasificación peirceana de los signos
Presentemos ahora una breve explicación de la clasificación de los signos que usaremos como base para el desarrollo de este artículo1. A lo largo de su carrera filosófica, Peirce produjo múltiples revisiones, ampliaciones y reducciones a su teoría del significado. Por ejemplo, con respecto a las clasificaciones de los signos, produjo la sintética categoría de tres tipos de signos que usaremos aquí: índices, iconos y símbolos, pero también una exhaustiva categorización de 66 tipos de signos (Borges, 2010). No obstante, su noción general del signo se estructura gracias a la siguiente tricotomía: una relación sígnica se compone del signo propiamente dicho, un interpretante y un objeto. En términos generales, el signo, también llamado representamen, es el vehículo que permite la significación. Este puede ser físico o mental, pero aquí nos ocuparemos solo de signos físicos. Una visualización de datos pertenece a estos últimos porque, a través de cualidades o rasgos formales –el color, el tamaño, la forma, la composición, etc.– presentes en su medio –el papel, la pantalla, etc.– permite que una persona desencadene una interpretación. El objeto, por su parte, es la cosa que el signo está representando. Por ejemplo, un mapa es un signo que tiene como objeto un territorio. Sin embargo, cabe decir que dentro de esta teoría un objeto no es solo lo que entendemos cotidianamente por objeto físico, también puede serlo un concepto, una construcción cognitiva, o el insight que se busca con las visualizaciones. Finalmente, el interpretante es el acto que conecta al signo con su objeto. Traído a terminología contemporánea, podríamos decir que el interpretante es un desarrollo cognitivo, el proceso de ver, pensar, imaginar, etc. que permite que el signo encuentre una interpretación en la mente, una idea a la cual anclarse. Así, desencadenar una interpretación puede entenderse como una sucesión de interpretantes que se convierten en signos de otros interpretantes.
La clasificación que diferencia a los signos como índices, iconos y símbolos está estructurada de acuerdo a su relación con su objeto. A grandes rasgos, hablamos de iconos cuando existe una semejanza con el objeto, de índices cuando se guarda una relación de contacto directo o causalidad con el objeto, y de símbolos cuando la relación se origina en el hábito o la convencionalidad. Es así como podemos también hablar de visualizaciones indéxicas, icónicas y simbólicas, si entendemos que ellas son signos que pueden operar bajo estas formas relacionales. Esa es la clasificación que busca desarrollar este texto.
Hay que decir que dichas categorías no son excluyentes, es decir: que un signo sea de cierto tipo no impide que sea además de otro tipo. Es, de hecho, común que en nuestra vida cotidiana nos encontremos con signos que funcionan simultáneamente como índices, iconos y símbolos. Igualmente, las visualizaciones de datos suelen combinar todas las formas de relación. Sin embargo, para los fines de este artículo, separaremos estas categorías para entender mejor qué posibilidades, dificultades y diferencias ofrecen para las Humanidades.
2.3. Tres versiones del concepto de dato
Por otro lado, también es necesario hacer una aclaración con respecto a los múltiples sentidos que ha tenido y tiene el término dato. Como bien ha sido estudiado por Allés Torrent (2019) y por Rosenberg (2013), el término significa diferentes cosas dependiendo de la actividad en la que se busca aplicar, y, adicionalmente, su sentido general ha cambiado históricamente. Aquí se justifica mencionar tres de los sentidos que nos servirán para establecer distinciones importantes en el artículo. Por una parte, está el dato propiamente dicho, es decir, la percepción empírica de un acontecimiento, de un aspecto del mundo como nos es dado directamente a nuestra percepción. Un dato, en este sentido, es una evidencia, o es, por así decirlo, una muestra de la verdad y la realidad. De acuerdo con Rosenberg (2013) esta concepción empírica es históricamente reciente: en el siglo XVII se concebía que el dato ya estaba dado por una fuerza anterior a los humanos –Dios o las matemáticas–, y solo hasta el siglo XVIII empieza a tener un uso regular como algo que se obtiene a partir de la experimentación y observación científica.
Por otra parte, tenemos el dato entendido como datatype, es decir, como la forma en la que se codifica la información operable por computadores en los lenguajes de programación. Este puede entenderse como un elemento primitivo, una pieza fundamental y atómica con la que pueden construirse luego archivos más complejos (Flanders & Jannidis, 2018). Los datatypes más comunes son la información numérica –por ejemplo, los números enteros y decimales de punto flotante–, la del tipo booleana –que define si se cumplen o no condiciones de verdad: falso o verdadero– y los caracteres –una versión codificada de un alfabeto–. Estos pueden, a su vez, componer estructuras de datos más complejas que, a partir de sus configuraciones, constituyen las arquitecturas de operación y de interacciones que definen nuestras formas de actuar con los computadores (Manovich, 2013). Por ejemplo, una secuencia de datos numéricos puede codificar los colores que se mostrarán en una pantalla, o una secuencia de caracteres puede codificar lo que los humanos podemos leer como palabras. Sin embargo, las cadenas de caracteres, o strings, no son estrictamente palabras o frases, en el sentido en el que no tienen semántica para el computador –la palabra cultura puede codificarse como una cadena de caracteres: ["c", "u", "l", "t", "u", "r", "a"], no así su significado–. Aunque un computador puede guardar como información una secuencia de letras, este por sí mismo no puede entender la diferencia semántica que existe entre una palabra y otra. Lo mismo sucede con los colores y con infinidad de signos que sólo tienen sentido para los seres humanos; las máquinas solo realizan operaciones sobre los datatypes, pero no entienden el significado que pueden desencadenar las representaciones que producen.
Por último, tenemos el dato entendido como unidad operable estadísticamente. Bajo este sentido tenemos datos categóricos (ordinales y nordinales) y numéricos (Munzner, 2015). Los primeros expresan la pertenencia de un objeto a un conjunto, y son, por definición, discretos. Por ejemplo, que un texto sea prosa o verso es una distinción categórica. Al igual que con los datatypes, con los datos estadísticos no se toma en consideración la diferencia semántica en las categorías, solo se usan como contenedores de objetos diferenciables. En cambio, los datos numéricos expresan una cantidad medible en alguna de las cualidades del objeto. Por proponer un caso, en un corpus la extensión en palabras promedio de los versos puede compararse con la extensión en palabras promedio de los textos en prosa. Es decir, se puede producir un dato numérico a partir de contar la frecuencia de cada categoría. Esta diferenciación entre categóricos y numéricos es importante en estadística porque ayuda a determinar qué tipo de operaciones son posibles con qué tipos de datos. Pensemos que, a pesar de que las fechas se expresan con números, no son realmente numéricas sino categóricas ordinales, pues siguen una secuencia ordenada pero no se pueden promediar, o no tendría sentido hacerlo. Son, al final, conjuntos de diferenciación que tienen una estructura secuencial pero no son cantidades en el sentido estricto. Es esencial afirmar que los datos de la investigación en Humanidades, en su gran mayoría, se codifican como datos categóricos, y por tal motivo no se prestan tan fácilmente a los análisis estadísticos como otras disciplinas más cuantificables: digamos, las Finanzas o la Física. Así, la visualización de datos no se puede reducir a la seguridad y la estandarización estable de los procesos sobre datos numéricos. A pesar de que los datos categóricos son contables y se puede establecer su frecuencia, no podríamos afirmar que su sentido más complejo está simplemente en ese conteo, como se hace evidente con los problemas semánticos que surgen al tratar de explicar las particularidades de un texto sólo a través de determinar la frecuencia de ciertas palabras. La polisemia, la ambigüedad y la densidad del sentido desaparecen con la generalización categórica.
3. VISUALIZACIONES ICÓNICAS, INDÉXICAS Y SIMBÓLICAS
Una vez cubiertos los fundamentos teóricos que dan forma a este artículo podemos hacer un recorrido por distintos tipos de visualizaciones de acuerdo a la clasificación peirceana de los signos.
3.1. Visualizaciones icónicas
Los signos icónicos son aquellos en los que el signo guarda una relación de semejanza con su objeto. Aunque en la tradición semiótica existe una discusión de larga data acerca de lo que quiere decir realmente que algo tenga semejanza (Eco, 2017), aquí podemos quedarnos con un concepto del sentido común: dos cosas son semejantes si comparten algunas cualidades entre sí. Como lo ve Peirce, los signos icónicos están estrechamente relacionados con el pensamiento abstracto. En su artículo La esencia de la matemática (1974), Peirce afirma que la abstracción hipostática es el proceso de pensamiento mediante el cual tomamos un percepto y lo concebimos como un objeto en sí mismo, lo hipostasiamos. Por ejemplo, tomar la expresión La miel dulce y extraer el adjetivo dulzura para considerarlo como un objeto de pensamiento por sí solo. Así, si tenemos en nuestra mente un inventario de cualidades abstractas, podemos ver cómo un objeto es semejante o no a otro. Por ejemplo, el azúcar y la miel son semejantes en el sentido en el que tienen la cualidad abstracta de la dulzura. Un signo icónico se parece a lo que representa de esta misma manera. Por ejemplo, una foto en un documento se parece a una persona en ciertos aspectos: el color, la forma, la disposición; pero no en otros, el tamaño, la bidimensionalidad, etc.
A pesar de que existe una larga historia de la gráfica de información o la visualización de datos, muy anterior a la aparición de tales términos para nombrarla y a la creación de las tecnologías computacionales (Rendgen, 2019), la estrategia contemporánea más establecida de la visualización de datos está basada en la lógica de los signos icónicos y en la abstracción de la información. Podemos afirmar que el libro The semiology of graphics del cartógrafo Jacques Bertin (2011), publicado originalmente en 1968, es el precursor de las estrategias más difundidas de la visualización de datos contemporánea. Allí Bertin hizo explícita la idea de que las visualizaciones son transformaciones gráficas de la información abstracta que extraemos del mundo, es decir, son representaciones icónicas. Posteriormente, Lelan Wilkinson, en su libro The Grammar of Graphics (2013), publicado originalmente en 1999, refinó los procedimientos y estableció lo que llamó álgebra de la visualización. A saber, un sistema de transformaciones formales que permiten convertir los datos en gráficos legibles. Debido a esta herencia, aunque existe una literatura cada vez más extensa con respecto a la visualización de datos, la mayoría de la teoría se centra en un proceso puramente icónico: el mapeo de datos en marcas y canales visuales. Es decir, en la proyección de datos en formas gráficas que son equivalentes, que guardan una relación de parecido con la información a través de la abstracción hipostática. La gran mayoría del software enfocado en la producción de gráficos basados en información se orienta bajo principios icónicos: por ejemplo, el paquete ggplot2, del lenguaje de programación estadístico R, justamente toma su nombre, sus dos primeras letras, de la noción del grammar of graphics; o la librería D3 (Data Driven Documents), la base de buena parte del software de visualización para el lenguaje JavaScript, y por lo tanto de la internet, es una aplicación estricta de los principios de Wilkinson.
Bajo esta perspectiva icónica, por un lado, los datos deben extraerse de una manera que permita su formalización. Léase, que puedan convertirse en datatypes y que puedan manipularse como datos estadísticos. Luego, se toma un conjunto de primitivos visuales llamados marcas – básicamente, el punto, la línea y el plano– y se transforman ciertos canales o cualidades visuales de esas marcas –la posición, el color, el tamaño, la forma, la inclinación, la cantidad– (ver figura1). Así, digamos, un gráfico de barras transforma un conjunto de datos numéricos en el alto o el ancho de un conjunto de barras. Es decir, transforma el canal del tamaño de una serie de planos de acuerdo a una correspondencia abstracta con los datos. Un gráfico de torta o pie transforma una serie de datos de proporción en ángulos de planos con forma de arco que, como resultado, deben construir un círculo completo. Un gráfico de línea transforma datos continuos en posiciones de marcas con respecto a un eje. Todos estos ejemplos, bastante ortodoxos, por cierto, son icónicos: se parecen a o guardan semejanza con lo que buscan representar bajo un aspecto abstracto hipostasiado.
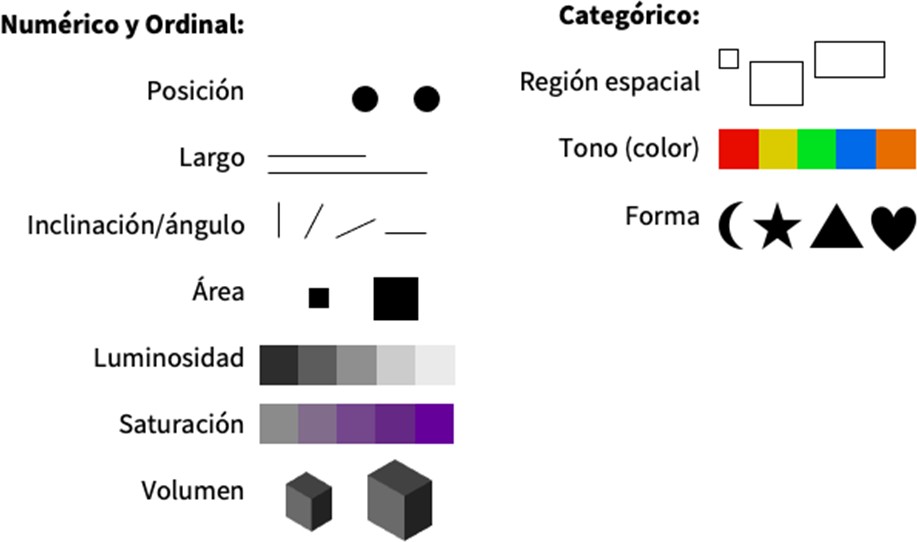
Fuente: elaboración propia
Como propone Wilkinson (2013), podemos entender este tipo de visualizaciones como una función matemática: la información formalizada se encuentra en un dominio, y existe otro codominio que contiene equivalencias formales en términos de marcas visuales y canales (figura 2). Un dato tiene equivalencia en posición, en color, en forma, etc. en el mundo del gráfico. La tarea de quien produce la visualización está en escoger la función correcta, la transformación adecuada para representar el dato, el sistema de conexiones entre dominio y codominio. Así, la visualización icónica es un proceso regulado y protocolizado que evita las ambigüedades y se establece como una herramienta universalizante. No es gratuito que Wilkinson llamara a su estrategia álgebra de la visualización, pues se plantea como una manera consistente matemáticamente de convertir cantidades numéricas y conjuntos discretos en gráficos sin ambigüedades y con procedimientos claramente definidos.
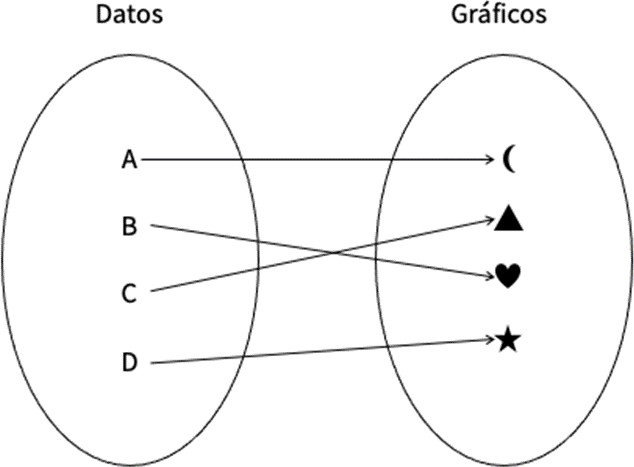
Fuente: elaboración propia
Como lo afirma Lattmann (2018), los modelos son construcciones icónicas que buscan representar aspectos de semejanza de un objeto parcialmente, pero que tienen el beneficio de poder hacer evidentes rasgos que no serían captados fácilmente. Consideremos un ejemplo. Las gráficas que se presentan en las figuras 3, 4 y 5 son visualizaciones icónicas de dos tipos de datos obtenidos a partir del procesamiento del catálogo razonado digital de la artista colombiana Beatriz González2. El primer tipo de dato es una clasificación categórica de la paleta de colores predominantes en cada una de las obras presentes en el catálogo. Cada paleta de colores predominantes está compuesta por diez colores en formato RGB obtenidos usando la librería Color Thief3 del lenguaje de programación JavaScript. Posteriormente, los datos RGB de las paletas fueron convertidos por aproximación en datos categóricos, usando la siguiente lista de doce colores: amarillo, azul, blanco, cian, gris, gris claro, gris oscuro, naranja, negro, rojo, rosa y verde. El segundo tipo de dato es el conteo numérico de la presencia de los colores seleccionados en las paletas de colores. Cada una de las visualizaciones utiliza los mismos datos, pero corresponde a una función visual diferente: la figura 3 es un gráfico de barras que transforma el conteo en el largo de las barras, la número 4 es un gráfico de dona que transforma cada conteo en un ángulo acumulativo, y la 5 es un treemap que transforma el conteo en un área rectangular. Todas las gráficas transforman los datos categóricos en colores equivalentes al color que representan. Como se puede observar, las tres gráficas permiten captar con mayor o menor precisión que existe una preponderancia de colores grises en la obra de Beatriz González –aunque esto se debe principalmente a artefactos de la digitalización: el color de fondo en esculturas o el color de papel en dibujos–, y que hay una preferencia por ciertos matices particulares, como el rosa, el naranja, el rojo y el cian
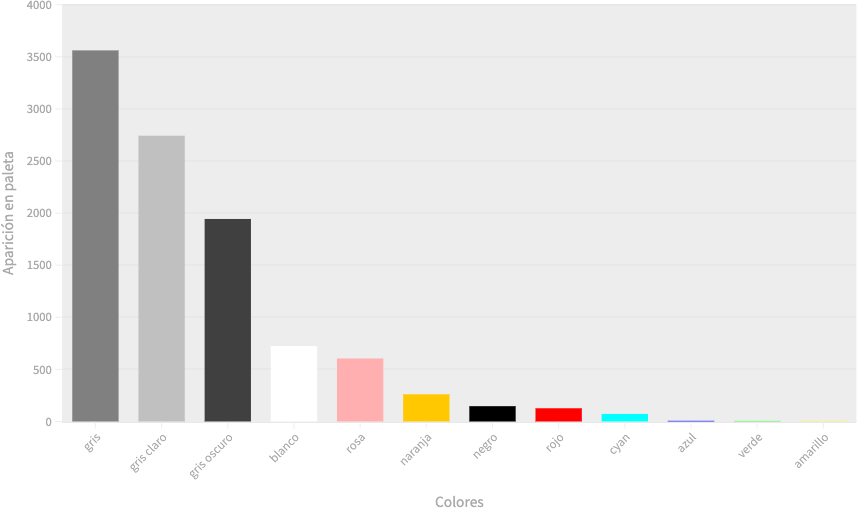
Fuente: elaboración propia
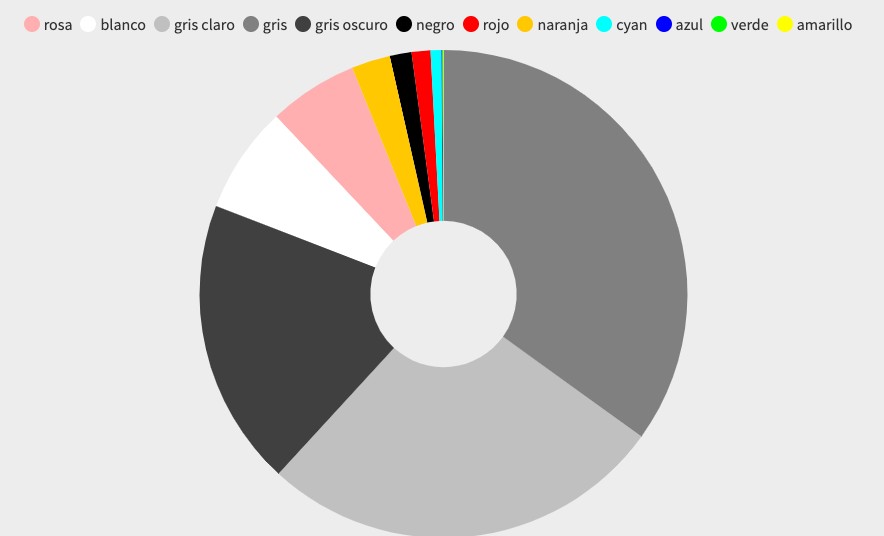
Fuente: elaboración propia

Fuente: elaboración propia
En este punto cabe advertir que las presuposiciones de las que parte la estrategia de la visualización icónica son problemáticas para las Humanidades. Como lo afirma Johanna Drucker (2011; 2020), debemos ser reflexivos frente a dos condiciones importantes que dan forma a los gráficos de información: por una parte, los datos no son una réplica transparente de las cualidades del mundo. En otras palabras, siempre hay interpretación por parte de un sujeto que recolecta los datos o que diseña la recolección automatizada. Frente a esta circunstancia, Drucker (2011) ha propuesto que el término data debería reemplazarse por el término capta, con el fin de hacer énfasis en el carácter subjetivo del acto de la recolección; este es, como vimos, el sentido contemporáneo del dato como proceso empírico. Es justamente la idea de abstracción hipostática la que hace evidente tal condición de la recolección de datos: hipostasiar requiere necesariamente una separación selectiva de las cualidades de un objeto. Tal selección omite otras cualidades que pueden ser relevantes o que pueden permitir insights diferentes. Desde el punto de vista de Drucker, la función algebraica de la transformación de datos no es realmente transparente ni consistente, a pesar de que se defienda como un proceso mecanizado y universalizante, pues son sujetos quienes construyen los algoritmos, quienes toman decisiones frente a la transformación de los datos. Por ejemplo, como afirma Matthew Edney (2019) en su libro Cartography, the Ideal and its History, la cartografía convencional, que apunta a valores de representación propiamente icónicos con elementos simbólicos, omite que la creación de mapas es un acto humano, culturalizado, que contiene la idiosincracia, los sesgos y los ideales que, asumidos como universales, ocultan parte importante de la visualización como objeto cultural. Por otra parte, como lo afirma Drucker, este tipo de gráficos se dirigen a un público, que también producirá interpretaciones dependiendo de sus capacidades cognitivas y sus sesgos particulares. La doble condición subjetiva de la recolección y la transformación de datos y la lectura de los gráficos debe hacerse explícita en la lógica de la visualización, y debe considerarse como algo que necesariamente introduce ambigüedad a su proceso aparentemente transparente (figura 6). Tal ambigüedad no es negativa desde un punto de vista humanístico, es, por el contrario, parte esencial de los procesos de comunicación. Así, aquí debemos afirmar que la aproximación noreflexiva frente a la subjetividad es insostenible para las Humanidades, pues este campo del conocimiento se define justamente por la consciencia acerca de la cultura y la producción humana, por el desarrollo de las subjetividades. Adoptar sin cuestionamientos una postura en la que se asumen los datos como transformaciones mecanicistas de datos capturados ciegamente es claramente antihumanística.
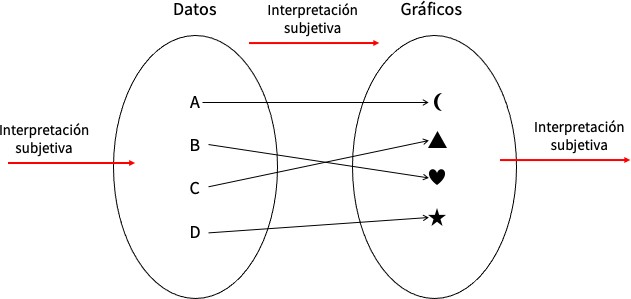
Fuente: elaboración propia
A raíz de su proyección como herramienta científica, la predominante estrategia icónica en la visualización ha desencadenado un creciente interés por la precisión en la lectura. Por ejemplo, el influyente estudio de Cleveland y McGill (1984) estableció los parámetros de una serie de investigaciones que intentan definir principios generales acerca de cómo deben construirse gráficos para que las personas que las lean puedan, primero, extraer la mayor cantidad de información relevante y, segundo, retener esa información en la memoria de la manera más eficiente. De forma similar, el estadístico Edward Tufte (1983) se convirtió en un influyente proponente de una serie de principios que promueven una lectura determinista y estricta de la visualización, libre de elementos irrelevantes y de codificaciones innecesarias. El estilo tuftiano ha definido una estrategia objetivista que elimina las minucias semánticas de la representación gráfica. No obstante, también existen propuestas que tratan de aliviar las ausencias presentes en las formas tradicionales de visualizar datos icónicamente. Por ejemplo, Drucker (2011) propone la creación de sistemas de coordenadas variables, que no sigan series geométricas regulares sino percepciones subjetivas con respecto al paso del tiempo o a la distribución del espacio (figura 7). Similarmente, el trabajo de las diseñadoras Giorgia Lupi y Stefanie Posavec (2018) contrasta con los gráficos mínimos del estilo tuftiano. Las obras de Lupi y Posavec (2018) siguen las ideas principales de la visualización icónica –la recolección de datos y la transformación en formas visuales por medio de funciones– pero de una manera en la que siempre es evidente que el proceso requiere de interpretación, tanto por parte de quien produce la gráfica como de quien la lee. Tal efecto se logra a partir de subvertir las convenciones típicas que se han considerado hasta ahora como buenas prácticas en la visualización –la eliminación del factor humano, podría decirse–: usar reglas no convencionales, aparentemente arbitrarias, pero que dan cuenta de que la creación de la interfaz de la visualización es también un proceso de conocimiento y de expresión. La figura 8 muestra un ejemplo basado en un ejercicio propuesto por Lupi y Posavec, la visualización de la percepción subjetiva de la intensidad y la temática de una canción a través del tiempo. El ejemplo está basado en la canción De donde vengo yo del grupo musical ChocQuibTown4. Gracias a la gráfica es posible notar cierta regularidad en la intensidad musical, que aumenta hacia el final de la canción. También se hace evidente una estructura temática que gira alrededor de las dicotomías culturales que el grupo musical señala con respecto a la región Pacífica en Colombia.

Fuente: elaboración propia

Fuente: elaboración propia
3.2. Visualizaciones indéxicas
Los signos indéxicos son aquellos en los que el signo guarda una relación con su objeto gracias a un contacto directo o una causalidad. Por ejemplo, las huellas en la arena son signos indéxicos del caminar de un transeúnte. O, puesto de una manera ligeramente diferente, diríamos que nuestra interpretación de tales huellas es que fueron causadas por el contacto directo del transeúnte al pisar la arena. Ver las huellas conduce a una secuencia de interpretantes a través de la cual suponemos una causalidad. Si lo vemos así, los signos indéxicos tienen una lógica particular que los diferencia de otros tipos de signos: nos permiten hacer conjeturas acerca de un acontecimiento que probablemente ya no está, o que no percibimos directamente, pero que ha dejado marcas interpretables. Entendemos las marcas, las ruinas, las huellas, las cicatrices, etc. como evidencia histórica de un acontecimiento previo, suponemos que el índice es una muestra de que algo pasó de verdad, o suponemos que el índice es un aspecto de una totalidad mayor que es inaccesible. En términos generales, los índices suelen ser parciales, pues el contacto con el objeto deja señales incompletas que requieren de una conjetura por parte de la persona que las lee. La literatura detectivesca es especialmente hábil en usar índices para mantener la narrativa de la historia; solo al final sabemos si nuestras especulaciones fueron correctas y si estábamos, por lo tanto, leyendo hábilmente cada uno de los signos que llevan a la resolución del evento.
Los signos indéxicos están relacionados con el pensamiento abductivo, una habilidad cognitiva esencial en los seres humanos (Peirce, 1992a). La abducción, en contraposición a la deducción y la inducción, es el modo de razonamiento en el que se establecen conexiones razonables a través de elementos que no están estrictamente conectados por consecuencias lógicas o reglas estadísticas. Es, en otras palabras, el pensamiento hipotético, especulativo, conjetural, que surge a partir de la invención de una explicación que debe verificarse con la adquisición de más información. Puede decirse que los signos indéxicos, a través del razonamiento abductivo, nos permiten llegar a un nuevo conocimiento por proxy (Floridi, 2015), o por aproximación, en el sentido en el que nos acercan a un fenómeno desde variables indirectas. Por ejemplo, los síntomas son proxies de la existencia de una enfermedad.
Así, las visualizaciones indéxicas son aquellas que no han pasado por el tamizaje previo de la transformación del dato –en su sentido empírico– en datatype o dato estadístico. Por el contrario, la visualización indéxica es causada directamente por un acontecimiento. Entonces, en este caso, es el registro de marcas o huellas dejadas por el objeto que se quiere estudiar. De acuerdo con Offenhuber y Telhan (2018), este tipo de visualización es el que guarda mayor cercanía ontológica con el tema de estudio, pues obedece a la causalidad directa; el objeto de estudio no ha sido filtrado por la captura y la formalización en los formatos operables de los datos. A diferencia de la estrategia icónica, no existe una función matemática que produzca las cualidades visuales de una imagen indéxica. Existe, si se quiere, una función de contacto, que define cómo se capturarán rastros del acontecimiento o del fenómeno. Esta función de contacto depende de la invención y el ingenio de quien va a crear gráficos para un problema particular, pues no existen métodos estándar para construir visualizaciones indéxicas.
Observemos un ejemplo, la superposición de una serie de obras en acuarela en formato horizontal del pintor costumbrista colombiano Ramón Torres Méndez5 (figura 9). La superposición fue obtenida a través de un proceso de suma de colores con el software abierto ImageJ, siguiendo el proceso descrito por Ferguson (2017). A través del uso directo del objeto que queremos estudiar –la serie de obras propiamente–, y a través del proceso de disponer en una sola imagen todo el conjunto visual, redujimos la producción a un solo momento, a una sola imagen que conjuga toda la obra. Este es un ejemplo de sampleo o muestreo, es decir, de la extracción de fragmentos directos del objeto para obtener una versión reducida en términos de información. También es un ejemplo de síntesis por medio de superposición. Estos dos métodos constituirían la función de contacto elegida. Las cualidades de las pinturas no han sido procesadas en datos estadísticos, y lo que tenemos es, más bien, una especie de promedio indéxico, una huella dejada por la luz de la exposición de todas las imágenes, similar al método fotográfico clásico de la múltiple exposición. Tal proceso nos permite hacer conjeturas sobre el estilo del artista, sobre decisiones de composición, e incluso sobre el contenido de las obras, como se observa en la figura 10. Aunque esta visualización indéxica es más difícil de leer que las transparentes visualizaciones icónicas, optimizadas para abstraer lo estrictamente necesario, con un poco de esfuerzo abductivo se puede ver que las pinturas comparten ciertas decisiones estilísticas: bordes difusos, en ocasiones marcos ornamentados, representaciones de personas y animales, cierta tendencia a la centralidad, etc

Fuente: elaboración propia

Fuente: elaboración propia
3.3. Visualizaciones simbólicas
Los signos simbólicos son, finalmente, los signos que tienen relación con su objeto por hábito o por convención. A diferencia de los signos indéxicos e icónicos, se puede decir que los símbolos son arbitrarios o nomotivados. En otras palabras, en principio, un agente que interpreta puede reconocer por su propia cuenta una causalidad en un índice o un parecido en un icono basándose en su propia experiencia individual, pero no necesariamente puede encontrarle sentido a un símbolo sobre el que no ha aprendido previamente a través de la adquisición de convenciones sociales. El ejemplo paradigmático de este tipo de signos es el lenguaje natural. Para entender las palabras que están dispuestas en esta página es necesario haber aprendido el código del español, pues el sentido de estas palabras no guarda relación con su objeto por contacto ni semejanza; no hay conjetura o relación abstracta que sea útil sin un adiestramiento previo.
Los símbolos son, por excelencia, los signos de la cultura, pues es a través de hábitos construidos en comunidad que podemos tener lenguaje, artes, historia, etc. y que, metafóricamente hablando, podemos comunicarnos con generaciones anteriores o futuras a la nuestra. Son, entonces, la constitución de acuerdos genéricos que permiten conservar información, establecer coordinación social, y dar continuidad a los sistemas culturales –como lo afirma Tomasello (2013), en su historia de los orígenes del lenguaje. Las visualizaciones simbólicas, por lo tanto, serían las representaciones gráficas capaces de dar cuenta de la construcción del hábito social, de las complejidades semánticas que establece la cultura, y las relaciones intertextuales entre distintas producciones humanas. Tales visualizaciones son especialmente problemáticas para la computación, pues, como afirmamos antes, los datatypes operables por máquinas y los datos estadísticos no son capaces de establecer distinciones de significado. Por el contrario, las distinciones semánticas suelen quedar consignadas en metadatos anotados por expertos. Sin embargo, como veremos, a pesar de esta limitante, es posible utilizar ciertas estrategias para facilitar a los seres humanos interpretaciones fructíferas.
Aunque no pertenecen a la ortodoxia de las visualizaciones icónicas que han dominado el software de computación, existe una elaborada tradición de estrategias visuales usadas para comprender las complejidades de la cultura en la investigación humanística. Un caso importante es el proyecto del historiador de arte Aby Warburg llamado Atlas Mnemosyne o atlas de la memoria (Warburg, 2010). A finales del siglo XIX y principios del siglo XX, Warburg emprendió la tarea investigativa de encontrar rastros de iconografía pagana en obras del Renacimiento italiano. Para ello creó una serie de paneles con imágenes que reunió bajo criterios de similaridad formal y conceptual. Al realizar lo que aquí llamaremos una colección adyacente, Warburg, mucho antes de que se hablara del campo de la visualización de datos y sin los masivos archivos digitales de internet, logró seguir los fines que hacíamos explícitos al comienzo del artículo: produjo signos –el panel en su totalidad– que ayudaban a un ser humano –a él o a otros investigadores– a ampliar su cognición a través de la selección y disposición temática de elementos diversos. El montaje adyacente de una colección temática es una estrategia de visualización simbólica que permite traer a escala humana, a través de la conjunción espacial atemporal, una extensión enorme de producción cultural, y le permitió a Warburg, de hecho, establecer parte de los fundamentos de la iconografía contemporánea y crear conexiones entre las representaciones artísticas del pasado y el presente (figura 11).

Fuente: The Warburg Institute
Además de su importancia para el campo específico de la historia del arte, la estrategia de Warburg es adecuada para la investigación humanística en general, y merece una atención especial en la búsqueda de unas visualizaciones fructíferas que se adapten a los intereses investigativos de las humanidades, porque es un método que permite activar con naturalidad los enormes archivos de documentación que registran el pasado. Crear colecciones y disponerlas en un espacio conjunto de percepción visual permite aprovechar las posibilidades del archivo digital sin ocultar el papel de la audiencia en la construcción de significado. En otras palabras, la colección adyacente facilita la creación de conexiones simbólicas para una audiencia porque hace más evidentes las construcciones implícitas de hábitos y tradiciones culturales. Como lo afirmaba Peirce, los símbolos crecen (Short, 2007), es decir, su significado se amplía en la medida en la que se enriquecen las lecturas, los usos cambian y las comunidades complejizan las lectuas, una colección es una captura inmediata de ese proceso. A manera de ejemplo, la figura 12 representa un ejercicio, inspirado en el trabajo de Warburg, en el que se toman diferentes representaciones europeas del continente americano y se disponen junto a imágenes comerciales o de la cultura popular en las que se puede encontrar una iconografía y una serie de códigos simbólicos transversales. Particularmente, la representación alegórica colonialista de América como una mujer semidesnuda que sostiene materias primas y naturaleza tropical

Fuente: elaboración propia
La colección adyacente es un ejercicio interpretativo que requiere de cierto bagaje cultural o de una exploración curiosa de documentos en archivos; así, la computación no suple la construcción de un hilo conductor del sentido o del diseño del gráfico, sino que facilita la recolección y conjunción de elementos dispersos. Sin embargo, como complemento a la colección adyacente pueden producirse otras formas de visualización que ayudan a complejizar las relaciones simbólicas de una manera más concreta y direccionada a través de abstracciones icónicas que procuran conservar estructuras simbólicas. Las visualizaciones de redes relacionales como los grafos y los árboles son, en este sentido, el complemento ideal para la estrategia warburgiana. Como afirma Newman (2010), "una red es una representación simplificada que reduce un sistema a una estructura abstracta que captura solo lo básico de patrones de conexión y poco más" (p.2). Por ejemplo, los grafos, de los que existe un amplio estudio de sus topologías y sus configuraciones matemáticas (Ortega Guerrero, 2016), son una estrategia que permite ver, de una forma relativamente sencilla, relacionamientos concretos como guiños intertextuales o conexiones entre elementos narrativos. A manera de ejemplo, la figura 13 presenta un grafo que sintetiza los personajes más relevantes dentro de los capítulos que componen la historia del Diario de Lecumberri de Álvaro Mutis (1975) junto con las referencias intertextuales que utiliza Mutis para describir a algunos de los personajes
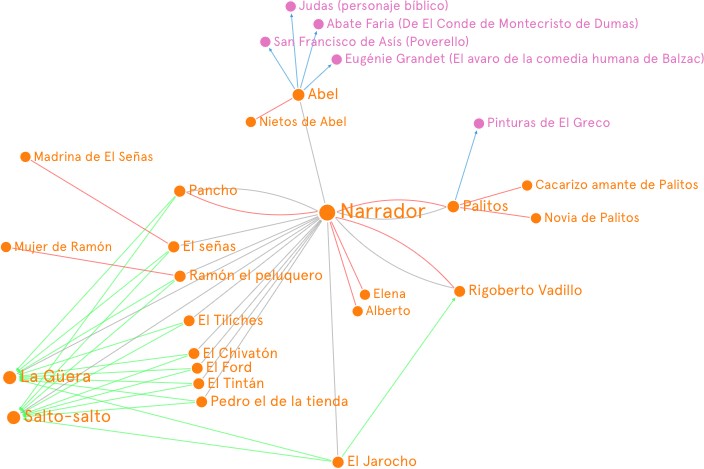
Fuente: elaboración propia
4. CONCLUSIONES
Este artículo tuvo como propósito establecer una clasificación de la visualización de datos útil para entender las particulares necesidades de las Humanidades Digitales. Para construir la clasificación se utilizó el modelo sígnico del filósofo y semiólogo Charles S. Peirce, que establece que los signos se pueden dividir en signos icónicos, indéxicos y simbólicos. Como se desarrolló a lo largo del texto, cada tipo particular de signo tiene una lógica diferente en cuanto a la relación con su objeto y, en consecuencia, implica unas formas de significado concretas que definen ventajas y desventajas para la visualización de datos humanísticos. No obstante, como se afirmó antes, la clasificación propuesta es en cierta medida artificial, pues asume cada tipo de signo como una entidad diferenciada, aun cuando en la experiencia real es común encontrar gráficos que contienen relaciones que corresponden a todos los tipos de signos. Entonces, más que privilegiar una estrategia sobre otra, aquí vale decir que para producir visualizaciones de datos es necesario tener en cuenta todos los tipos de signos y sus posibilidades de mezcla de una manera que permita que las imágenes propicien la extensión de la cognición y la percepción a escala humana en la investigación humanística.
El artículo también procuró defender la idea de que las HD deben asimilar, difundir y generalizar las estrategias que se adaptan mejor al estudio de la cultura, más que apropiar irreflexivamente los métodos de otros campos del conocimiento. Especialmente, debemos insistir en hacer explícitas las subjetividades en la recopilación de datos y su transformación, y en aprovechar tales subjetividades para enriquecer los sentidos de los signos visuales que apoyan la investigación.
La visualización de datos tiene una historia más extensa que la de la Computación, a pesar de que haya ganado mayor fuerza su teorización a partir de la creación de software especializado y de la cultura visual de internet. Esta nueva fuerza ha traído consigo una preponderancia de la estrategia icónica que es insuficiente para captar los igualmente importantes y complejos sentidos indéxicos y simbólicos de la cultura humana. Siguiendo esta línea, cabe cerrar estas conclusiones afirmando que las Humanidades Digitales pueden mirar al pasado para encontrar los métodos nocomputacionales de visualización de datos que han existido tradicionalmente en la práctica académica. Estos métodos pueden dar luces a las nuevas estrategias computacionales que le permitirán dar justa cuenta de los sentidos de sus objetos de estudio. Este artículo buscó ser un aporte en esa dirección. Un camino para investigación futura puede estar direccionado en el desarrollo de software especializado para la visualización de datos humanísticos que equilibren los métodos icónicos, indéxicos y simbólicos, y que sean flexibles con respecto a la subjetividad en la recolección, transformación e interpretación de los datos.
REFERENCIAS BIBLIOGRÁFICAS
Allés Torrent, S. (2019). Sobre la complejidad de los datos en Humanidades, o cómo traducir las ideas a datos. Revista de Humanidades Digitales, 4, 1-28. https://doi.org/10.5944/ rhd.vol.4.2019.24679
Bertin, J. (2011). Semiology of Graphics: Diagrams, Networks, Maps. ESRI Press.
Borges, P. (2010). A Visual Model of Peirce’s 66 Classes of Signs Unravels His Late Proposal of En- larging Semiotic Theory. En L. Magnani, W. Carnielli, y C. Pizzi (Eds.), Model-Based Reason- ing in Science and Technology: Abduction, Logic, and Computational Discovery (pp. 221-237). Springer. https://doi.org/10.1007/978-3-642-15223-8_12
Clark, A., & Chalmers, D. (1998). The Extended Mind. Analysis, 58(1), 7-19. https:// doi.org/10.1093/analys/58.1.7
Cleveland, W. S., & McGill, R. (1984). Graphical Perception: Theory, Experimentation, and Appli- cation to the Development of Graphical Methods. Journal of the American Statistical Associa- tion, 79(387), 531-554. JSTOR. https://doi.org/10.2307/2288400
Drucker, J. (2020). Visualization and interpretation: Humanistic approaches to display. The MIT Press.
Drucker, J. (2011). Humanities Approaches to Graphical Display. Digital Humanities Quarterly, 5(1).
Eco, U. (2017). Kant y el ornitorrinco. Debolsillo.
Edney, M. H. (2019). Cartography: The ideal and its history. The University of Chicago Press.
Fauconnier, G., & Turner, M. (2003). The way we think: Conceptual blending and the mind’s hidden complexities. Basic Books.
Ferguson, K. L. (2017). Digital Surrealism: Visualizing Walt Disney Animation Studios. Digital Hu- manities Quarterly, 11(1).
Flanders, J., & Jannidis, F. (2018). The Shape of Data in Digital Humanities: Modeling Texts and Text- based Resources. Routledge.
Floridi, L. (2015). A Proxy Culture. Philosophy & Technology, 28(4), 487-490. https:// doi.org/10.1007/s13347-015-0209-8
Lattman, C. (2018). Iconizing the Digital Humanities. Models and Modeling froma Semiotic Perspec- tive. Historical Research, Suplement, 31, 124-146. https://doi.org/10.12759/hsr.suppl.31.2018.124-146
Lupi, G., & Posavec, S. (2018). Observe, collect, draw!: A visual journal: Discover the patterns in your everyday life. Princeton Architectural Press.
Manovich, L. (2013). Software Takes Command: Extending the Language of New Media. Bloomsbury.
Munzner, T. (2015). Visualization analysis and design. CRC Press, Taylor & Francis Group.
Mutis, A. (1975). Diario de Lecumberri / La mansión de Araucaíma. Círculo de lectores.
Newman, M. E. J. (2010). Networks: An introduction. Oxford University Press.
Offenhuber, D., & Telhan, O. (2018). Indexical Visualization – The Data-less Information Display. En U. Ekman, J. D. Bolter, L. Diaz, M. Søndergaard, & M. Engberg (Eds.), Ubiquitous computing, complexity, and culture (pp. 288-302). Routledge, Taylor & Francis Group.
Ortega Guerrero, J. C. (2016). Las redes sociales y su modelado matemático. Revista Ensayos Pedagógicos, 19-35. https://doi.org/10.15359/rep.esp-16.1
Peirce, C. S. (1992a). On the Logic of Drawing History from Ancient Documents, Especially from Tes- timonies. En The essential Peirce: Selected philosophical writings (pp. 75-114). Indiana Univer- sity Press.
Peirce, C. S. (1992b). What is a sign? En The essential Peirce: Selected philosophical writings (pp. 4- 10). Indiana University Press.
Peirce, C. S. (1974). La esencia de la matemática. En J. R. Newman (Ed.), La forma del pensamiento matemático. Grijalbo. https://www.unav.es/gep/EssenceMathematics.html
Rendgen, S. (2019). History of information graphics. Taschen.
Rosenberg, D. (2013). Data before the Fact. En L. Gitelman (Ed.), «Raw Data» Is an Oxymoron (pp.15-40). The MIT Press.
Scolari, C. A. (2004). Hacer clic: Hacia una sociosemiótica de las interacciones digitales. Gedisa.
Short, T. L. (2007). Peirce’s Theory of Signs. Cambridge University Press.
Tomasello, M. (2013). Los orígenes de la comunicación humana. Katz.
Tufte, E. R. (1983). The Visual Display of Quantitative Information. Graphics Press.
Warburg, A. (2010). Atlas Mnemosyne. Akal.
Wilkinson, L. (2013). The Grammar of Graphics. Springer Science & Business Media.

 https://orcid.org/0000-0002-1631-4747
https://orcid.org/0000-0002-1631-4747